
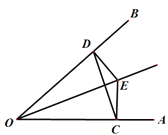
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,连接C、D.
(1)求证:OC=OD;
(2)请确定射线OE与线段CD 的位置关系,并说明理由.
【答案】见解析
【解析】试题分析:(1)由已知条件易得∠EDO=∠ECO=90°,DE=CE,从而得到∠EDC=∠ECD,进一步得到∠ODC=∠OCD,最后可由“等边对等角”得到OC=OD(也可通过证△ODE≌△OCE来证明OC=OD);
(2)由(1)可知OC=OD,DE=CE,从而可证得OE是CD的垂直平分线得到结论.
试题解析:(1)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴ DE=CE,∠EDO=∠ECO=90°,
∴∠EDC=∠ECD,
∴∠EDO-∠EDC=∠ECO-∠ECD,即∠ODC=∠OCD,
∴OC=OD.
(2) 射线OE垂直平分线段CD,理由如下:
由(1)可得:DE=CE,OC=OD
∴点E和点O都在线段CD的垂直平分线上,
∴射线OE垂直平分线段CD.
∴ 射线OE与线段CD的位置关系是互相垂直.


科目:初中数学 来源: 题型:
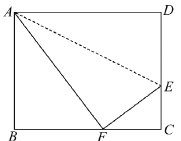
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5cm, 且tan∠EFC=,那么矩形ABCD的周长_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
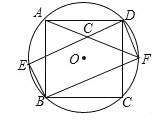
【题目】(2016山东潍坊第21题)正方形ABCD内接于⊙O,如图所示,在劣弧![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
(1)四边形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=12cm,AC=6cm.动点E从A点出发以3cm/s沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.当点E经过______s时,△DEB与△BCA全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.
(1)线段OC的长为 ;
(2)求证:△CBD≌△COE;
(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1,其中点O,B,D,E的对应点分别为点O1,B1,D1,E1,连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.
①当1<a<2时,请直接写出S与a之间的函数表达式;
②在平移过程中,当S=![]() 时,请直接写出a的值.
时,请直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
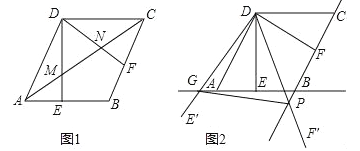
【题目】(2016山东潍坊第24题)如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN=![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
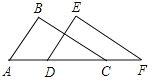
A. ∠BCA=∠F B. ∠B=∠E C. BC∥EF D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
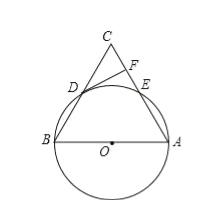
【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com