
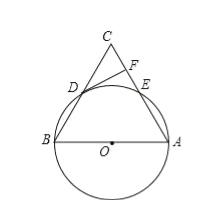
【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD,由切线的性质即可得出∠ODF=90°,再由BD=CD,OA=OB可得出OD是△ABC的中位线,根据三角形中位线的性质即可得出,根据平行线的性质即可得出∠CFD=∠ODF=90°,从而证出DF⊥AC;(2)由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°,再结合OB=OD可得出△OBD是等边三角形,根据弧长公式即可得出结论.
试题解析:(1)证明:连接OD,如图所示.

∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°.
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴DF⊥AC.
(2)解:∵∠CDF=30°,
由(1)得∠ODF=90°,
∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴![]() 的长=
的长=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
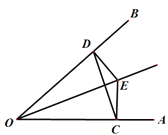
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,连接C、D.
(1)求证:OC=OD;
(2)请确定射线OE与线段CD 的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A=2x2+x,B=kx2-(3x2-x+1).
(1)当x= -1时,求A的值;
(2)小明认为不论k取何值,A-B的值都无法确定.小红认为k可以找到适当的数,使代数式A-B的值是常数.你认为谁的说法正确?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
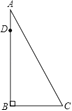
【题目】如图,AB为一棵大树,在树上距地面10米的D处有两只猴子,他们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C处,已知两只猴子所经路程都为15米,求树高AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com