
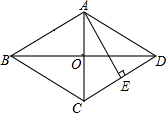
 如图,在菱形ABCD中,对角线AC,BD相交于点O,AE⊥CD,垂足为E,且AE=OB,求∠CAE的度数.
如图,在菱形ABCD中,对角线AC,BD相交于点O,AE⊥CD,垂足为E,且AE=OB,求∠CAE的度数. 科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD是平行四边形,BE⊥AC于点E,DF⊥AC于点F.连接BF、DE,试判断四边形BFDE是什么样的四边形?并说明理由.
如图,已知四边形ABCD是平行四边形,BE⊥AC于点E,DF⊥AC于点F.连接BF、DE,试判断四边形BFDE是什么样的四边形?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对重庆某中学初2017级全体学生中考体考成绩的调查 | |
| B. | 为制作某校学生校服,对该校2017级某班学生的身高情况进行调查 | |
| C. | 对元宵节重庆市市场上彩色汤圆质量情况的调查 | |
| D. | 对用于发射卫星的运载火箭各零部件的检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
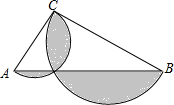 如图,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为$\frac{5}{2}$π-4.
如图,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为$\frac{5}{2}$π-4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com