
| A. | 对重庆某中学初2017级全体学生中考体考成绩的调查 | |
| B. | 为制作某校学生校服,对该校2017级某班学生的身高情况进行调查 | |
| C. | 对元宵节重庆市市场上彩色汤圆质量情况的调查 | |
| D. | 对用于发射卫星的运载火箭各零部件的检查 |
分析 根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
解答 解:A、对重庆某中学初2017级全体学生中考体考成绩的调查适合采用全面调查方式;
B、为制作某校学生校服,对该校2017级某班学生的身高情况进行调查适合采用全面调查方式;
C、对元宵节重庆市市场上彩色汤圆质量情况的调查适合采用抽样调查方式;
D、对用于发射卫星的运载火箭各零部件的检查适合采用全面调查方式;
故选:C.
点评 本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:选择题
 如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是( )
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是( )| A. | (0,21008) | B. | (21008,21008) | C. | (21009,0) | D. | (21009,-21009) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
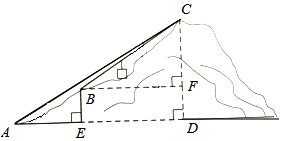 游客上歌乐山山有两种方式:一种是如图,先从A沿登山步道走到B,再沿索道乘座缆车到C,另一种是沿着盘山公路开车上山到C,已知在A处观铡到C,得仰角∠CAD=3l°,且A、B的水平距离AE=430米,A、B的竖直距离BE=210米,索道BC的坡度i=1:1.5,CD⊥AD于D,BF⊥CD于F,则山篙CD为( )米;(参考数据:tan31°≈0.6.cos3l°≈0.9)
游客上歌乐山山有两种方式:一种是如图,先从A沿登山步道走到B,再沿索道乘座缆车到C,另一种是沿着盘山公路开车上山到C,已知在A处观铡到C,得仰角∠CAD=3l°,且A、B的水平距离AE=430米,A、B的竖直距离BE=210米,索道BC的坡度i=1:1.5,CD⊥AD于D,BF⊥CD于F,则山篙CD为( )米;(参考数据:tan31°≈0.6.cos3l°≈0.9)| A. | 680 | B. | 690 | C. | 686 | D. | 693 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com