
分析 (1)根据阅读材料中的方法得出结果即可;
(2)原式第一个括号中各项分母有理化后,计算即可得到结果.
解答 解:(1)根据题意得:$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\frac{\sqrt{n}-\sqrt{n-1}}{(\sqrt{n}+\sqrt{n+1})(\sqrt{n}-\sqrt{n-1})}$=$\sqrt{n}$-$\sqrt{n-1}$;
(2)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2012}$-$\sqrt{2011}$)($\sqrt{2012}$+1)=($\sqrt{2012}$-1)($\sqrt{2012}$+1)=2012-1=2011.
故答案为:(1)$\sqrt{n}$-$\sqrt{n-1}$
点评 此题考查了分母有理化,弄清阅读材料中分母有理化的方法是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 对重庆某中学初2017级全体学生中考体考成绩的调查 | |
| B. | 为制作某校学生校服,对该校2017级某班学生的身高情况进行调查 | |
| C. | 对元宵节重庆市市场上彩色汤圆质量情况的调查 | |
| D. | 对用于发射卫星的运载火箭各零部件的检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
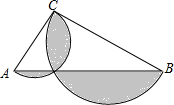 如图,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为$\frac{5}{2}$π-4.
如图,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,则图中阴影部分的面积为$\frac{5}{2}$π-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数a,b在数轴上的对应点如图所示,则下列式子中:①-b>a;②|b|<|a|;③a-b>a+b;④|a|+|b|>|a-b|,正确的有( )
有理数a,b在数轴上的对应点如图所示,则下列式子中:①-b>a;②|b|<|a|;③a-b>a+b;④|a|+|b|>|a-b|,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com