
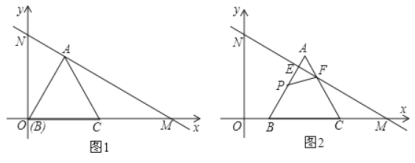
【题目】如1,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,等边
,等边![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,
重合,![]() 边落在
边落在![]() 轴正半轴上,点
轴正半轴上,点![]() 恰好落在线段
恰好落在线段![]() 上,将等边
上,将等边![]() 从图1的位置沿
从图1的位置沿![]() 轴正方向以每秒1个单位长度的速度平移,边
轴正方向以每秒1个单位长度的速度平移,边![]() 分别与线段
分别与线段![]() 交于点
交于点![]() (如图2所示),设
(如图2所示),设![]() 平移的时间为
平移的时间为![]() (s).
(s).
(1)![]() ,等边
,等边![]() 的边长为 ;
的边长为 ;
(2)在运动过程中,当![]() 为何值时,MN垂直平分AB;
为何值时,MN垂直平分AB;
(3)在![]() 开始平移的同时,点
开始平移的同时,点![]() 从
从![]() 的顶点
的顶点![]() 出发,以每秒2个单位长度的速度沿折线
出发,以每秒2个单位长度的速度沿折线![]() 运动,当点
运动,当点![]() 运动到
运动到![]() 时立即停止运动,
时立即停止运动,![]() 也随之停止平移.
也随之停止平移.
①当点![]() 在线段
在线段![]() 上运动时,若
上运动时,若![]() ,求
,求![]() 的值;
的值;
②当点![]() 在线段
在线段![]() 上运动时,若
上运动时,若![]() 的面积
的面积![]() ,求
,求![]() 的值.
的值.
【答案】(1)30°,3;(2)3;(3)①![]() 或
或![]() ;②2
;②2
【解析】
(1)根据,∠OMN=30°和△ABC为等边三角形,求证△OAM为直角三角形,然后即可得出答案.
(2)易知当点C与M重合时直线MN平分线段AB,此时OB=3,由此即可解决问题;
(3)①分为点P在EF下方和P在EF上方两种情况讨论,分别表示出PE和AE,用AE=2PE,即可解得t值;
②确定好点P的表示,表示出EF,及P到EF的高度,用三角形面积公式,即可解得t值.
(1)∵直线MN分别与x轴正半轴、y轴正半轴交于点M、N,
∴OM=6cm,ON=![]() ,
,
∴tan∠OMN=![]() =
=![]() ,
,
∴∠OMN=30°,
∴∠ONM=60°,
∵△ABC为等边三角形,
∴∠AOC=60°,∠NOA=30°,
∴OA⊥MN,即△OAM为直角三角形,
∴OA=![]() OM=
OM=![]() ×6=3.
×6=3.
故答案为30°,3.
(2)若直线MN垂直平分AB,则MN与![]() 中过点C的高重合
中过点C的高重合
故当点C与M重合时直线MN平分线段AB,此时![]() ,
,
又![]() 右移的速度为每秒1个单位,所以t=3.
右移的速度为每秒1个单位,所以t=3.
故答案为3.
(3)①由题意知BP=2t,BM=6﹣t,
∵∠BEM=90°,∠BME=30°,
∴BE=3﹣![]() ,AE=AB﹣BE=
,AE=AB﹣BE=![]() ,
,
若P在EF下方
则![]()
∵![]()
∴![]() ,即
,即![]()
若P在EF上方,
则![]()
∵![]()
∴![]() ,即
,即![]()
故![]() 的值为:
的值为:![]() 或
或![]()
②由BP=2t,BM=6﹣t,
∵∠BEM=90°,∠BME=30°,
∴BE=3﹣![]() ,AE=AB﹣BE=
,AE=AB﹣BE=![]() ,
,
∵![]()
∴![]() ,
,![]()
∴![]()
∴P到EF的高![]()
∴![]() ,解得
,解得![]() 或
或![]()
∵P的匀速速度为每秒2个单位,AB=3,
∴P在AC上时,![]()
∴![]() .
.
故t的值为:2


科目:初中数学 来源: 题型:
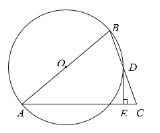
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点 D作DE⊥AC,垂足为E.
(1)求证:DE是⊙O的切线.
(2)若⊙O的半径为2,∠A=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求一棵甲种树苗和一棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动。校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如下图所示:

根据以上信息,解答下列问题:
(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为 ;
(2)求本次所抽取学生四月份“读书量”的平均数;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水产公司有一种海产品共2104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
售价 | 400 | 300 | 250 | 240 | 200 | 150 | 125 | 120 |
销售量 | 30 | 40 | 48 | 50 | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用反比例函数刻画这种海产品每天的销售量![]() (千克)与销售价格
(千克)与销售价格![]() (元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量
(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量![]() (千克)与销售价格
(千克)与销售价格(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段BC上有两点E,F,在线段CB的异侧有两点A,D,满足AB=CD,AE=DF,CE=BF,连接AF;
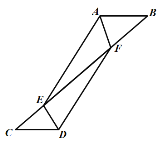
(1)连接DE,求证:四边形AEDF是平行四边形;
(2)若∠B=40°,∠DFC=30°,当AF平分∠BAE时,求∠BAF.
查看答案和解析>>
科目:初中数学 来源: 题型:
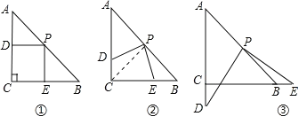
【题目】操作:在△ABC中,AC=BC=4,∠C=90°,将一块直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。如图①、②、③是旋转三角板得到的图形中的3种情况。
探究:
(1)如图①,PD⊥AC于D,PE⊥BC于E,则重叠部分四边形DCEP的面积为___,周长___.
(2)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②加以证明;
(3)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传普及新冠肺炎防治知识,引导学生做好防控.某校举行了主题为“防控新冠,从我做起”的线上知识竞赛活动,测试内容为20道判断题,每道题5分,满分100分.为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩.已知抽查得到的八年级的数据如下:
80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
为了便于分析数据,统计员对八年级数据进行了整理,得到了表一:
成绩等级 | 分数(单位:分) | 学生数 |
|
| 5 |
|
|
|
|
|
|
|
| 2 |
八、九年级成绩的平均数、中位数、优秀率如下:(分数80分以上、不含80分为优秀)
年级 | 平均数 | 中位数 | 优秀率 |
八年级 | 77.5 |
|
|
九年级 | 76 | 82.5 | 50% |
(1)根据题目信息填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)八年级王宇和九年级程义的分数都为80分,请判断王宇、程义在各自年级的排名哪位更靠前?请简述你的理由;
(3)八年级被抽取的20名学生中,获得![]() 等和
等和![]() 等的学生将被随机选出2名,协助学校普及新冠肺炎防控知识,求这两人都为
等的学生将被随机选出2名,协助学校普及新冠肺炎防控知识,求这两人都为![]() 等的概率.
等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com