【题目】在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．

（1）求抛物线的解析式；

（2）已知点D（m，m﹣2）在第三象限的抛物线上，求点D关于直线AB对称的点E的坐标；

（3）若点P是抛物线上的动点，点Q是直线y=﹣x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，求出相应点Q的坐标．

参考答案：

【答案】（1）y=x2+x﹣4；（2）E点坐标为（0，﹣2）；（3）综上所述，Q点的坐标为（﹣4，4）或（﹣2+2，2﹣2）．

【解析】

试题分析：（1）设交点式y=a（x+4）（x﹣2），然后把B点坐标代入求出a即可得到抛物线解析式；

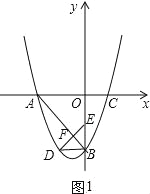
（2）先判断△AOB为等腰直角三角形得到∠ABO=45°，再把把D（m，m﹣2）代入y=x2+x﹣4求出m得到D（﹣2，﹣4），则利用D嗲和B点坐标可判断BD∥x轴，BD=2，如图1，根据对称的性质BE=BD=2，BF垂直平分DE，再判断点E在y轴上，于是利用OE=OB﹣BE=2可得到E点坐标；

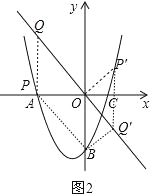
（3）如图2，根据平行四边形的判定方法当PQ=OB=4，PQ∥OB时，点P、Q、B、O为顶点的四边形为平行四边形，设Q（t，﹣t），则P（t， t2+t﹣4），分类讨论：当OQ为边时，四边形OQPB为平行四边形，则﹣t﹣（t， t2+t﹣4）=4，当OQ为对角线时，四边形OBQP为平行四边形，则t2+t﹣4﹣t=4，然后分别解方程求出t即可得到满足条件的Q点坐标．

试题解析：（1）设抛物线的解析式为y=a（x+4）（x﹣2），

把B（0，﹣4）代入得a4（﹣2）=﹣4，解得a=，

所以抛物线解析式为y=（x+4）（x﹣2），即y=x2+x﹣4；

（2）∵A（﹣4，0），B（0，﹣4），∴OA=OB，∴△AOB为等腰直角三角形，

∴∠ABO=45°，把D（m，m﹣2）代入y=x2+x﹣4得m2+m﹣4=m﹣2，解得m1=2，m2=﹣2，

∴D（﹣2，﹣4），而B（0，﹣4），∴BD∥x轴，BD=2，

∵点D和点E关于直线AB对称（DE交AB于F），如图1，

∴BE=BD=2，BF垂直平分DE，∴∠DBF=∠EBF=45°，∴∠DBE=90°，

∴点E在y轴上，而OE=OB﹣BE=2，

∴E点坐标为（0，﹣2）；

（3）判断有2个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形．如图2，

当PQ=OB=4，PQ∥OB时，点P、Q、B、O为顶点的四边形为平行四边形，

设Q（t，﹣t），则P（t， t2+t﹣4），

当OQ为边时，四边形OQPB为平行四边形，则﹣t﹣（t， t2+t﹣4）=4，解得t1=0（舍去），t2=﹣4，此时Q点坐标为（﹣4，4）；

当OQ为对角线时，四边形OBQP为平行四边形，则t2+t﹣4﹣t=4，解得t1=﹣2+2，t2=﹣2﹣2（舍去），此时Q点坐标为（﹣2+2，2﹣2），

综上所述，Q点的坐标为（﹣4，4）或（﹣2+2，2﹣2）．

关闭