
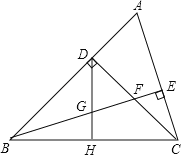
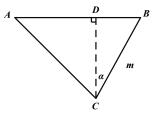
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD交于F,H是BC边的中点,连接DH与BE交于点G,则下列结论:
①BF=AC;②∠A=∠DGE;③CE<BG;④S△ADC=S四边形CEGH;⑤DGAE=DCEF中,正确结论的个数是( )
A.2B.3C.4D.5
【答案】C
【解析】
证明△BDF≌△CDA可判断①;
由![]() 利用三角形的外角的性质及四边形的内角和定理可判断②;
利用三角形的外角的性质及四边形的内角和定理可判断②;
连接![]() 利用DH是BC的垂直平分线,从而可判断③;
利用DH是BC的垂直平分线,从而可判断③;
过G作GJ⊥AB于J,过F作FM![]() BC于M,连接GM,设
BC于M,连接GM,设![]() 分别计算三角形ADC的面积和四边形CEGH的面积可判断④;
分别计算三角形ADC的面积和四边形CEGH的面积可判断④;
由△BDF∽△CEF,可判断⑤.
解:∵CD⊥AB,BF⊥AC,
∴∠BEC=∠BDC=∠ADC=90°,
∵∠ABC=45°,
∴∠DCB=45°=∠ABC,
∴BD=DC,
∵∠BDC=∠CEF=90°,∠DFB=∠EFC,
∴由三角形内角和定理得:∠DBF=∠ACD,
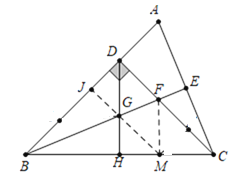
∵在△BDF和△CDA中,
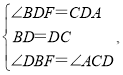
∴△BDF≌△CDA(ASA),
∴BF=AC,∠BFD=∠A,∴①正确;
∵∠DFB=∠FBC+∠FCB=∠FBC+45°,∠DGF=∠GBD+45°,∠FBC=∠GBD,
∴∠DFG=∠DGF,
![]()
![]()
![]()
![]()
∴∠A=∠DGE,故②正确,
如图,连接![]()
∵∠ABC=45°,∠BDC=90°,
∴△BDC是等腰直角三角形,
∵H是BC边的中点,
∴DH垂直平分BC,
![]()
![]()
![]()
![]() 故③正确;
故③正确;
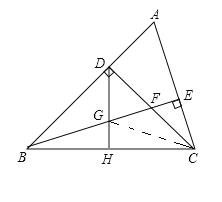
过G作GJ⊥AB于J,过F作FM![]() BC于M,连接GM,
BC于M,连接GM,
![]()
![]()
![]()
![]() 平分
平分![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形DGMF是菱形,
四边形DGMF是菱形,
![]()
设![]()
则![]()
![]()
![]() 四边形CFGH的面积=梯形GHMF的面积+
四边形CFGH的面积=梯形GHMF的面积+![]() 的面积
的面积
![]()
![]()
![]() S△ADC
S△ADC![]() S四边形CEGH,故④错误.
S四边形CEGH,故④错误.
∵△BDF∽△CEF,
∴![]() ,
,
∵BD=DC,CE=AE,DF=DG,
∴![]()
∴DGAE=DCEF,故⑤正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,小明在C处看到西北方向上有一凉亭A,北偏东![]() °的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=
°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=![]() 米,则A、B两点相距 ( )
米,则A、B两点相距 ( )
A.![]() 米B.
米B.![]() 米
米
C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
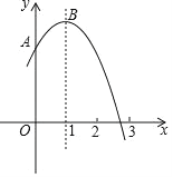
【题目】如图,抛物线y=-x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
①抛物线y=-x2+2x+m+1与直线y=m+2有且只有一个交点;
②若点M(-2,y1)、点N(![]() ,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;
,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=-(x+1)2+m;
④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为![]() .
.
其中正确判断有( )
A.①②③④B.②③④C.①③④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的图像经过点A(4,4),B(5,0)和原点O,点P为抛物线上的一个动点,过点P作x轴的垂线,垂足为D(m,0)(m>0),并与直线OA交于点C.
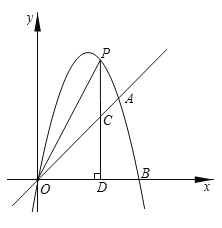
(1)求出抛物线的函数表达式;
(2)连接OP,当S△OPC=![]() S△OCD时,求出此时的点P坐标;
S△OCD时,求出此时的点P坐标;
(3)在直线OA上取一点M,使得以P、C、M为顶点的三角形与△OCD全等,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
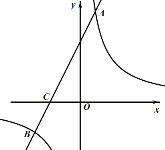
【题目】如图,在平面直角坐标系中,一次函数![]() (
(![]() ≠
≠![]() )的图象与反比例函数
)的图象与反比例函数![]() (
(![]() )的图象交于A、B两点,与
)的图象交于A、B两点,与![]() 轴交于C点,点A的坐标为(
轴交于C点,点A的坐标为(![]() ,6),点C的坐标为(-2,0),且
,6),点C的坐标为(-2,0),且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)利用图象求不等式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长分别为10cm和4cm的矩形纸片沿着虚线剪成两个全等的梯形纸片.裁剪线与矩形较长边所夹的锐角是45°,则梯形纸片中较短的底边长为( )
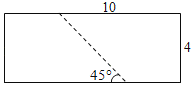
A.2cmB.2.5cmC.3cmD.3.5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com