
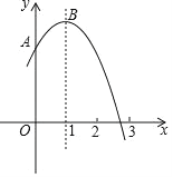
����Ŀ����ͼ��������y����x2��2x��m��1��mΪ��������y���ڵ�A����x���һ��������2��3֮�䣬����ΪB��
��������y����x2��2x��m��1��ֱ��y��m��2����ֻ��һ�����㣻
������M����2��y1������N��![]() ��y2������P��2��y3���ڸú���ͼ���ϣ���y1<y2<y3��
��y2������P��2��y3���ڸú���ͼ���ϣ���y1<y2<y3��
�۽�������������ƽ��2����λ��������ƽ��2����λ�����������߽���ʽΪy������x��1��2��m��
�ܵ�A����ֱ��x��1�ĶԳƵ�ΪC����D��E�ֱ���x���y���ϣ���m��1ʱ���ı���BCDE�ܳ�����СֵΪ![]() ��
��
������ȷ�ж��У� ��
A.�٢ڢۢ�B.�ڢۢ�C.�٢ۢ�D.�٢�
���𰸡�C
��������
�����κ����䷽��![]() �����жϢ٢ۣ���P���ݶԳ���ת�����Գ���������жϢڣ���m��1���뺯������ʽ��������A��C���꣬���ԳƸ�������֮���߶���̼��������ı���BCDE�ܳ�����Сֵ��
�����жϢ٢ۣ���P���ݶԳ���ת�����Գ���������жϢڣ���m��1���뺯������ʽ��������A��C���꣬���ԳƸ�������֮���߶���̼��������ı���BCDE�ܳ�����Сֵ��
�⣺��y����x2��2x��m��1��Ϊ����ʽΪ��![]()
�ඥ������Ϊ![]() ������ͼ����ֱ��y��m��2���У�ֻ��һ�������㣬����ȷ��
������ͼ����ֱ��y��m��2���У�ֻ��һ�������㣬����ȷ��
�������ϼ��¼�������Ҽ�����![]() ����ƽ��2����λ��������ƽ��2����λ�õ���
����ƽ��2����λ��������ƽ��2����λ�õ��� ![]() ������ȷ��
������ȷ��
���κ����ĶԳ�����ֱ��![]() ����P��2��y3���ɶԳƵ�
����P��2��y3���ɶԳƵ�![]() ���ڶԳ�����࣬y��x�����������
���ڶԳ�����࣬y��x�����������![]() ���ڴ���
���ڴ���
��m=1ʱ����������ʽΪ��![]() ����
����![]() ��
��![]() ��
��![]()
��B����y��ԳƵ�N����C����x��ԳƵ�M����![]() ����MN����MNΪBE��DE��CD�͵���Сֵ���ı���BCDE�ܳ���СֵΪMN��BC�ĺͣ����У�
����MN����MNΪBE��DE��CD�͵���Сֵ���ı���BCDE�ܳ���СֵΪMN��BC�ĺͣ����У�
![]()
�൱m��1ʱ���ı���BCDE�ܳ�����СֵΪ![]() ������ȷ��
������ȷ��
�ʴ�ѡ��C��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�ڣ�A��BΪx�������㣬��ABΪֱ���ġ�M��y����C��D���㣬CΪ![]() ���е㣬��AE��y���ڵ�F���ҵ�A������Ϊ��2��0����CD��8
���е㣬��AE��y���ڵ�F���ҵ�A������Ϊ��2��0����CD��8
��1�����M�İ뾶��
��2������P�ڡ�M��Բ�����˶���
����ͼ1����FP�ij������ʱ����P��ΪP����ͼ1�л�����P0���������P0������a��ֵ��
����ͼ1����EPƽ�֡�AEBʱ����EP�ij��ȣ�
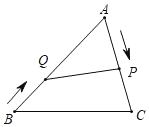
����ͼ2������D����M�����߽�x���ڵ�Q������P���A��B���غ�ʱ����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ���O������A��C��D����BC�ཻ�ڵ�E������AC��AE.����D��70�㣬���EAC�Ķ���Ϊ____________.
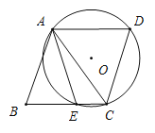
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
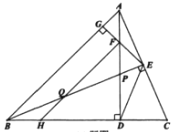
����Ŀ����ͼ����![]() �У�
�У�![]() ��������AD��BE���ڵ�P.����E��
��������AD��BE���ڵ�P.����E��![]() ������ΪG����AD�ڵ�F������F��
������ΪG����AD�ڵ�F������F��![]() ����BC�ڵ�H����BE���ڵ�Q������DE.
����BC�ڵ�H����BE���ڵ�Q������DE.
��1����![]() ��
��![]() ����DE�ij�
����DE�ij�
��2����![]() ����֤��
����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɱ߳�Ϊ1��С�����ι��ɵ�����ÿ��С�����εĶ���������.![]() �Ķ����ڸ���ϣ������̶ȳߵ�ֱ���ڸ��������л�ͼ����ͼ���������߱�ʾ����ͼ�����ʵ�߱�ʾ������������������⣺
�Ķ����ڸ���ϣ������̶ȳߵ�ֱ���ڸ��������л�ͼ����ͼ���������߱�ʾ����ͼ�����ʵ�߱�ʾ������������������⣺
(1)����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת90���õ��߶�
˳ʱ����ת90���õ��߶�![]() ��
��
(2)����![]() ���е�
���е�![]() ��
��
(3)����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ��ֱ��д��
��ֱ��д��![]() ��ֵ��
��ֵ��
(4)��![]() �ϻ���
�ϻ���![]() ������
������![]() ��ʹ
��ʹ![]() ��
��
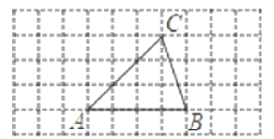
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB=16cm��AC=12cm������P��Q�ֱ���ÿ��2cm��1cm���ٶ�ͬʱ��ʼ�˶������е�P�ӵ�A��������AC��һֱ�Ƶ���CΪֹ����Q�ӵ�B������BA��һֱ�Ƶ���AΪֹ������P�����C��Q�����˶���
��1����ֱ���ú�t�Ĵ���ʽ��ʾAP�ij���AQ�ij�����д��������
��2����t���ں�ֵʱ����APQ����ABC���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ϊ�˴ٽ����ѣ�ij�̳������һ�ִ��������һ������������������ĸ���ͬ��С�����Ϸֱ������10Ԫ������20Ԫ������30Ԫ������40Ԫ�����������涨���ڱ��̳�ͬһ���ڣ��˿�ÿ������500Ԫ���Ϳ������������Ⱥ�����������(��һ�������Ż�)���̳�������С��������ĺͷ�����ȼ۸�Ĺ���ȯ������ȯ�����ڱ��̳����ѣ�ij�˿պ�����500Ԫ��
(1)��˳�����ɵõ�______Ԫ����ȯ��
(2)�����û���״ͼ���б��ķ���������ù˿�����ù���ȯ�Ľ�����60Ԫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ABC��45����CD��AB�ڵ�D��BEƽ�֡�ABC����BE��AC�ڵ�E����CD����F��H��BC�ߵ��е㣬����DH��BE���ڵ�G�������н��ۣ�
��BF��AC���ڡ�A����DGE����CE��BG����S��ADC��S�ı���CEGH����DGAE��DCEF�У���ȷ���۵ĸ����ǣ�������
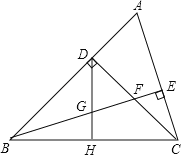
A.2B.3C.4D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=![]() ��x��0����ͼ����һ�κ���y=ax��2��a��0����ͼ���ڵ�A��3��n����
��x��0����ͼ����һ�κ���y=ax��2��a��0����ͼ���ڵ�A��3��n����
��1����ʵ��a��ֵ��
��2����һ�κ���y=ax��2��a��0����ͼ����y�ύ�ڵ�B������C��y���ϣ���S��ABC=2S��AOB�����C�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com