
����Ŀ���������Ϊ�˴ٽ����ѣ�ij�̳������һ�ִ��������һ������������������ĸ���ͬ��С�����Ϸֱ������10Ԫ������20Ԫ������30Ԫ������40Ԫ�����������涨���ڱ��̳�ͬһ���ڣ��˿�ÿ������500Ԫ���Ϳ������������Ⱥ�����������(��һ�������Ż�)���̳�������С��������ĺͷ�����ȼ۸�Ĺ���ȯ������ȯ�����ڱ��̳����ѣ�ij�˿պ�����500Ԫ��
(1)��˳�����ɵõ�______Ԫ����ȯ��
(2)�����û���״ͼ���б��ķ���������ù˿�����ù���ȯ�Ľ�����60Ԫ�ĸ��ʣ�
���𰸡���1��70����2����������![]() Ԫ���ĸ���Ϊ
Ԫ���ĸ���Ϊ![]()
��������
��1��������֪���������30Ԫ��40Ԫ��ʱ�õ��Ĺ���ȯ��ࣻ
��2���оٳ�������������ù˿�����ù���ȯ�Ľ�����60Ԫ�������ռ��������Ķ��ټ��ɣ�
�⣺��1�������������20Ԫ��40Ԫ��ʱ�õ��Ĺ���ȯ��࣬
��һ����30+40=70Ԫ��
�ʴ�Ϊ��70��
��2���ñ����г����п��ܵĽ����
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
�ɱ����֪������![]() �ֿ��ܵĽ�����������ǵij����ǵȿ��ܵģ���������
�ֿ��ܵĽ�����������ǵij����ǵȿ��ܵģ���������![]() Ԫ����Ϊ�¼�
Ԫ����Ϊ�¼�![]() �����ķ������ֿ��ܣ�
�����ķ������ֿ��ܣ�
�����¼�![]() �����ĸ���
�����ĸ���![]() ��
��
����������![]() Ԫ���ĸ���Ϊ
Ԫ���ĸ���Ϊ![]() .
.


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
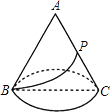
����Ŀ����ͼ��Բ��������DZ߳�Ϊ6cm����������ABC��P��ĸ��AC���е㣮����Բ�IJ����ϴ�B�㵽P������·�ߵij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
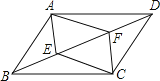
����Ŀ����ͼ��ƽ���ı���ABCD�У���E��F�ڶԽ���BD�ϣ���BE��DF����֤��
��1����ABE�ա�CDF��
��2���ı���AECF��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
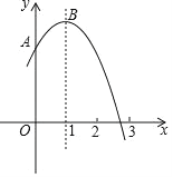
����Ŀ����ͼ��������y����x2��2x��m��1��mΪ��������y���ڵ�A����x���һ��������2��3֮�䣬����ΪB��
��������y����x2��2x��m��1��ֱ��y��m��2����ֻ��һ�����㣻
������M����2��y1������N��![]() ��y2������P��2��y3���ڸú���ͼ���ϣ���y1<y2<y3��
��y2������P��2��y3���ڸú���ͼ���ϣ���y1<y2<y3��
�۽�������������ƽ��2����λ��������ƽ��2����λ�����������߽���ʽΪy������x��1��2��m��
�ܵ�A����ֱ��x��1�ĶԳƵ�ΪC����D��E�ֱ���x���y���ϣ���m��1ʱ���ı���BCDE�ܳ�����СֵΪ![]() ��
��
������ȷ�ж��У� ��
A.�٢ڢۢ�B.�ڢۢ�C.�٢ۢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪˫����y=![]() ��ֱ��y=-x+2��P��˫���ߵ�һ������һ���㣬��P��y���ƽ���ߣ���ֱ��y=-x+2��Q�㣬OΪ����ԭ�㣮
��ֱ��y=-x+2��P��˫���ߵ�һ������һ���㣬��P��y���ƽ���ߣ���ֱ��y=-x+2��Q�㣬OΪ����ԭ�㣮
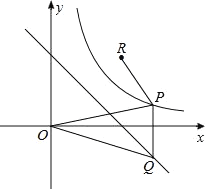

��1����ֱ��y=-x+2��������Χ�������ε��ܳ���
��2������PQO�����ΪS����S����Сֵ��
��3���趨��R��2��2�����Ե�PΪԲ�ģ�PRΪ�뾶����P�����P��ֱ��y=-x+2����M��N���㣮
���жϵ�Q���P��λ�ù�ϵ����˵�����ɣ�
����S��MON=S��PMNʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ߵ�ͼ����A(4��4)��B(5��0)��ԭ��O����PΪ�������ϵ�һ�����㣬����P��x��Ĵ��ߣ�����ΪD(m��0)(m>0)������ֱ��OA���ڵ�C��
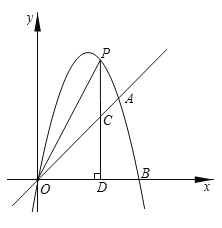
(1)��������ߵĺ�������ʽ��
(2)����OP����S��OPC��![]() S��OCDʱ�������ʱ�ĵ�P���ꣻ
S��OCDʱ�������ʱ�ĵ�P���ꣻ
(3)��ֱ��OA��ȡһ��M��ʹ����P��C��MΪ���������������OCDȫ�ȣ������M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2m+1��x+m2��2��0��
��1�����÷���������ʵ��������m����С����ֵ��
��2�������̵�����ʵ����Ϊx1��x2���ң�x1��x2��2+m2��21����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
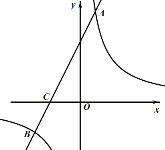
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() (
(![]() ��
��![]() )��ͼ���뷴��������
)��ͼ���뷴��������![]() (
(![]() )��ͼ����A��B���㣬��
)��ͼ����A��B���㣬��![]() �ύ��C�㣬��A������Ϊ(
�ύ��C�㣬��A������Ϊ(![]() ��6)����C������Ϊ(��2��0)����
��6)����C������Ϊ(��2��0)����![]() ��
��
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����B�����ꣻ
��3������ͼ����ʽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
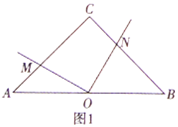
����Ŀ�����ⷢ�֣���1����ͼ1���ڵ���ֱ��������![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ��һ�㣬������
��һ�㣬������![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��������ϵΪ____��
��������ϵΪ____��
����̽������2����ͼ2���ڵ���������![]() �У�
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ��һ�㣬������
��һ�㣬������![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��������ϵ�Ƿ�ı䣬��˵�����ɣ�
��������ϵ�Ƿ�ı䣬��˵�����ɣ�
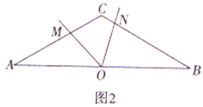
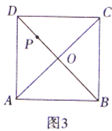
����������3����ͼ3����![]() Ϊ������
Ϊ������![]() �Խ��ߵĽ��㣬��
�Խ��ߵĽ��㣬��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬������
��һ�㣬������![]() ˳ʱ����ת
˳ʱ����ת![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() ���Ϊ
���Ϊ![]() ʱ��ֱ��д���߶�
ʱ��ֱ��д���߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com