
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.下列说法错误的是( )
(千米)的函数图象.下列说法错误的是( )
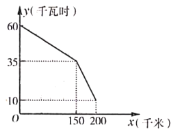
A.该汽车的蓄电池充满电时,电量是60千瓦时
B.蓄电池剩余电量为35千瓦时,汽车已行驶了150千米
C.当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时
D.25千瓦时的电量,汽车能行使![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙M,给出如下定义:若⊙M上存在两个点A,B,使AB=2PM,则称点P为⊙M的“美好点”.
(1)当⊙M半径为2,点M和点O重合时,
①点P1(-2,0),P2(1,1),P3(2,2)中,⊙O的“美好点”是______;
②点P为直线y=x+b上一动点,点P为⊙O的“美好点”,求b的取值范围;
(2)点M为直线y=x上一动点,以2为半径作⊙M,点P为直线y=4上一动点,点P为⊙M的“美好点”,求点M的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B,C,已知A(﹣1,0),C(0,3).
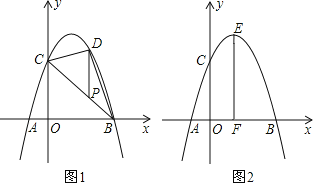
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一动点,过点P作y轴的平行线,交抛物线于点D,是否存在这样的P点,使线段PD的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+![]() MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.
MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() .
.
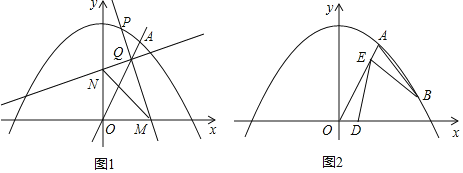
![]() 求直线
求直线![]() 的解析式和线段OA的长度;
的解析式和线段OA的长度;
![]() 点P为抛物线第一象限内的动点,过点P作直线PM,交x轴正半轴于点
点P为抛物线第一象限内的动点,过点P作直线PM,交x轴正半轴于点![]() 点M、O不重合
点M、O不重合![]() ,交直线OA于点Q,再过点Q作直线PM的垂线,交y轴正半轴于点N,连结MN,若
,交直线OA于点Q,再过点Q作直线PM的垂线,交y轴正半轴于点N,连结MN,若![]() ,试求
,试求![]() 及点Q的坐标;
及点Q的坐标;
![]() 如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上
如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上![]() 与点O、A不重合
与点O、A不重合![]() ,点
,点![]() 是x轴正半轴上的动点,且满足
是x轴正半轴上的动点,且满足![]() 继续探究:m取何值时,符合条件的E点的个数只有1个.
继续探究:m取何值时,符合条件的E点的个数只有1个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于
内接于![]() ,
,![]() ,直径
,直径![]() 交弦
交弦![]() 于点
于点![]() .
.
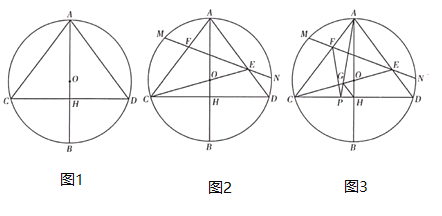
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,弦
,弦![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=![]() x+b与直线l2:y=kx+7交于点A(2,4),直线l1与x轴交于点C,与y轴交于点B,将直线l1向下平移7个单位得到直线l3,l3与y轴交于点D,与l2交于点E,连接AD.
x+b与直线l2:y=kx+7交于点A(2,4),直线l1与x轴交于点C,与y轴交于点B,将直线l1向下平移7个单位得到直线l3,l3与y轴交于点D,与l2交于点E,连接AD.
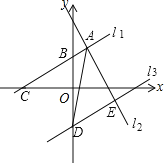
(1)求交点E的坐标;
(2)求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
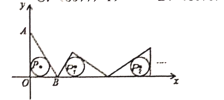
【题目】如图,把![]() 置于平面直角坐标系中,点A的坐标为
置于平面直角坐标系中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点P是
,点P是![]() 内切圆的圆心,将
内切圆的圆心,将![]() 沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合。第一次滚动后,圆心为
沿x轴的正方向作无滑动滚动,使它的三边依次与x轴重合。第一次滚动后,圆心为![]() ,第二次滚动后圆心为
,第二次滚动后圆心为![]() …依次规律,第2019次滚动后,
…依次规律,第2019次滚动后,![]() 内切圆的圆心
内切圆的圆心![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com