
【题目】对于平面直角坐标系xOy中的点P和⊙M,给出如下定义:若⊙M上存在两个点A,B,使AB=2PM,则称点P为⊙M的“美好点”.
(1)当⊙M半径为2,点M和点O重合时,
①点P1(-2,0),P2(1,1),P3(2,2)中,⊙O的“美好点”是______;
②点P为直线y=x+b上一动点,点P为⊙O的“美好点”,求b的取值范围;
(2)点M为直线y=x上一动点,以2为半径作⊙M,点P为直线y=4上一动点,点P为⊙M的“美好点”,求点M的横坐标m的取值范围.
【答案】(1)①P1,P2;②![]() ;(2)2≤m≤6.
;(2)2≤m≤6.
【解析】
利用圆的性质,圆的切线定理可依次推导出.
解:(1)①因为![]()
则有当AB最长为直径时,“美好点”在圆周上;
当AB小于直径时,2PM<直径,“美好点”在圆内.
所以点P的轨迹在圆内部和圆周上.
P1(-2,0)在圆上,P2(1,1)在圆内; P3(2,2)在圆外,所以选P1和P2.
②当直线![]() 与⊙O相切时,直线
与⊙O相切时,直线![]() 与X轴正向夹角为45°.
与X轴正向夹角为45°. 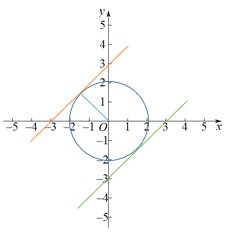
如图:直线![]() 与圆相切,则有
与圆相切,则有![]() 或
或![]() ;
;
∴![]() .
.
(2) 因为点M为直线![]() 上一动点, 点P作为⊙M的“美好点”又是直线
上一动点, 点P作为⊙M的“美好点”又是直线![]() 上一动点,
上一动点,
直线![]() 可以得到直线与X轴正向夹角为45°.
可以得到直线与X轴正向夹角为45°.
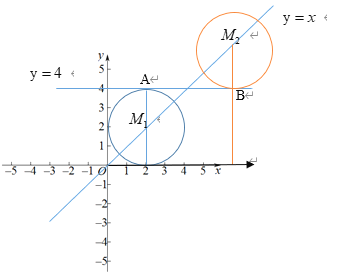
⊙M半径为2,考虑临界情况: ⊙M与![]() 相切
相切
∴当直线y=4与⊙M相切时,则有
M1在![]() 下方,此时M1横坐标即为2
下方,此时M1横坐标即为2
M2在![]() 上方, M2的横坐标为2+4=6.
上方, M2的横坐标为2+4=6.
∴![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
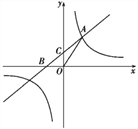
【题目】如图15,直线y=x+b与双曲线y=![]() 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠BCD=90°,ABCD=BCBD,BM∥CD交AD于点M.连接CM交DB于点N.
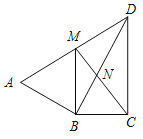
(1)求证:△ABD∽△BCD;
(2)若CD=6,AD=8,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 、点
、点![]() .
.
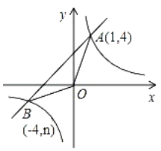
(1)求一次函数和反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)直接写出一次函数值大于反比例函数值的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为半径OA的上的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连结AF,AD.
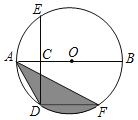
(1)求∠DAF的度数;
(2)若AB=10,求弦AD,AF和![]() 所围成的图形的面积.(结果保留π)
所围成的图形的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.小明所在的篮球队每月只参加一场比赛,共参加13场,则他参加的比赛中至少有两场比赛的举办月份相同
B.一次抽奖活动的中奖率是![]() ,那么抽100次必然会中一次奖
,那么抽100次必然会中一次奖
C.2019年11月29日是晴天,是必然事件
D.张老师从一个由2名男生和3名女生组成的小组中随机叫一名学生,叫到男生的可能性大于叫到女生的可能性
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市开展早市促销活动,为早到的顾客准备一份简易早餐,餐品为四样A:菜包、B:面包、C:鸡蛋、D:油条.超市约定:随机发放,早餐一人一份,一份两样,一样一个.
(1)按约定,“某顾客在该天早餐得到两个鸡蛋”是 事件(填“随机”、“必然”或“不可能”);
(2)请用列表或画树状图的方法,求出某顾客该天早餐刚好得到菜包和油条的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.下列说法错误的是( )
(千米)的函数图象.下列说法错误的是( )
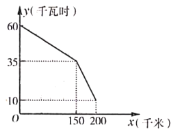
A.该汽车的蓄电池充满电时,电量是60千瓦时
B.蓄电池剩余电量为35千瓦时,汽车已行驶了150千米
C.当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时
D.25千瓦时的电量,汽车能行使![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com