
【题目】如图,AB是⊙O的直径,点C为半径OA的上的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连结AF,AD.
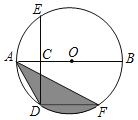
(1)求∠DAF的度数;
(2)若AB=10,求弦AD,AF和![]() 所围成的图形的面积.(结果保留π)
所围成的图形的面积.(结果保留π)
【答案】(1)∠DAF=30°;(2)弦AD,AF和![]() 所围成的图形的面积为
所围成的图形的面积为![]() π.
π.
【解析】
(1)根据平行线的性质得到∠EDF=∠ECB=90°,求得OC=![]() OE,于是得到结论;
OE,于是得到结论;
(2)连接OD、OF,于是得到∠DOF=2∠DAF=60°,根据扇形的面积公式即可得到结论.
(1)∵DF∥AB,CD⊥AB,
∴∠EDF=∠ECB=90°,
∴AB为⊙O的直径,
∵点C为半径OA的上的中点,
∴OC=![]() OE,
OE,
∴∠E=30°,
∴∠DAF=∠E=30°;
(2)连接OD,OF,
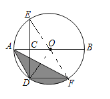
则∠DOF=2∠E=60°,
∵DF∥AB,
∴S△ADF=S△DOF,
∴S阴影=S扇形,
∵OD=![]() AB=5,
AB=5,
∴弦AD,AF和![]() 所围成的图形的面积=
所围成的图形的面积=![]() =
=![]() π.
π.


科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=α,E为对角线AC上的一点(不与A,C重合)将射线EB绕点E顺时针旋转β角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.
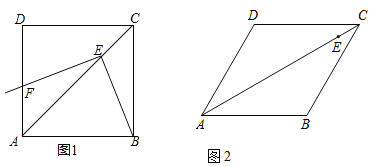
(1)如图1,当α=β=90°时,EB与EF的数量关系为 ;
(2)如图2,当α=60°,β=120°时,
①依题意补全图形;
②探究(1)的结论是否成立,若成立,请给出证明;若不成立,请举出反例证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,下面两图(图①、图②)是根据这组数据绘制的两种不完整的统计图,请你根据图中所提供的信息解答下列问题:
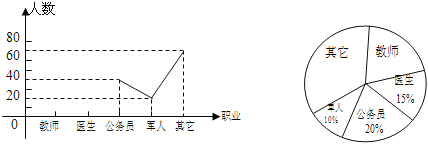
(1)求这次活动中一共调查了多少名学生.
(2)在扇形统计图中,求“教师”所在扇形的圆心角度数。
(3)补全两幅统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙M,给出如下定义:若⊙M上存在两个点A,B,使AB=2PM,则称点P为⊙M的“美好点”.
(1)当⊙M半径为2,点M和点O重合时,
①点P1(-2,0),P2(1,1),P3(2,2)中,⊙O的“美好点”是______;
②点P为直线y=x+b上一动点,点P为⊙O的“美好点”,求b的取值范围;
(2)点M为直线y=x上一动点,以2为半径作⊙M,点P为直线y=4上一动点,点P为⊙M的“美好点”,求点M的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:活动课上,某数学兴趣小组在操场看到马路上行驶的汽车,突发奇想:“想测量汽车的速度”.他们想到的方法是:如图,一人站在![]() 长且平行于公路(
长且平行于公路(![]() )的巨型广告牌(
)的巨型广告牌(![]() )前的点
)前的点![]() 处.广告牌恰好挡住了此人的视线,将看不到的那段公路记为
处.广告牌恰好挡住了此人的视线,将看不到的那段公路记为![]() .已知此人到广告牌和广告牌到公路的距离分别是
.已知此人到广告牌和广告牌到公路的距离分别是![]() 和
和![]() ,一辆匀速行驶的汽车经过公路
,一辆匀速行驶的汽车经过公路![]() 段的时间是
段的时间是![]() (不计汽车长度),请作答:
(不计汽车长度),请作答:
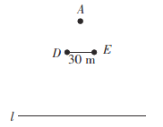
(1)请在图上画出线段![]() ;
;
(2)求该汽车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
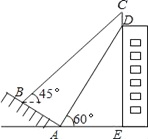
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,然后沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1: ![]() (斜坡的铅直高度与水平宽度的比),经过测量AB=10米,AE=15米.
(斜坡的铅直高度与水平宽度的比),经过测量AB=10米,AE=15米.
(1)求点B到地面的距离;
(2)求这块宣传牌CD的高度.(测角器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n).给出下列结论
①2a+c>0;
②若![]() 在抛物线上,则y1>y2>y3
在抛物线上,则y1>y2>y3
③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;
④当n=﹣![]() 时,△ABP为等腰直角三角形;
时,△ABP为等腰直角三角形;
其中正确结论个数有( )个.
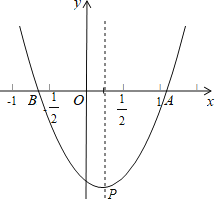
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于
内接于![]() ,
,![]() ,直径
,直径![]() 交弦
交弦![]() 于点
于点![]() .
.
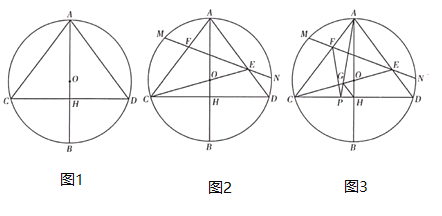
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,弦
,弦![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com