
【题目】如图,CD是⊙O的切线,点C在直径AB的延长线上.
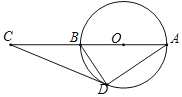
(1)求证:∠CAD=∠BDC;
(2)若BC=2,CD=3,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是
A. 红红不是胜就是输,所以红红胜的概率为![]()
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为![]()
D. 娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积![]() .
.
(3)在坐标轴上,是否存在点N,满足△BCN为直角三角形?如存在,请直接写出所有满足条件的点N.
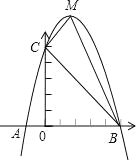
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为半径OA的上的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连结AF,AD.
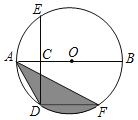
(1)求∠DAF的度数;
(2)若AB=10,求弦AD,AF和![]() 所围成的图形的面积.(结果保留π)
所围成的图形的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
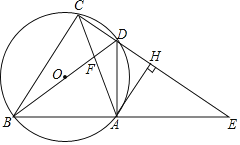
查看答案和解析>>
科目:初中数学 来源: 题型:
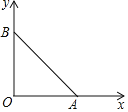
【题目】如图,![]() 的顶点A、B分别在x轴,y轴上,
的顶点A、B分别在x轴,y轴上,![]() ,且
,且![]() 的面积为8.
的面积为8.
![]() 直接写出A、B两点的坐标;
直接写出A、B两点的坐标;
![]() 过点A、B的抛物线G与x轴的另一个交点为点C.
过点A、B的抛物线G与x轴的另一个交点为点C.
![]() 若
若![]() 是以BC为腰的等腰三角形,求此时抛物线的解析式;
是以BC为腰的等腰三角形,求此时抛物线的解析式;
![]() 将抛物线G向下平移4个单位后,恰好与直线AB只有一个交点N,求点N的坐标.
将抛物线G向下平移4个单位后,恰好与直线AB只有一个交点N,求点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com