
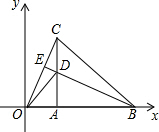
 如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=$\sqrt{2}$,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$).
如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=$\sqrt{2}$,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$). 分析 根据等腰三角形的性质,线段垂直平分线的性质,可得△ODC是等腰三角形,先根据等腰直角三角形的性质和勾股定理得到AC,BC,OB,OA,OC,AD,OD,CD,BD的长度,再根据相似三角形的判定与性质分两种情况得到BM的长度,进一步得到点M的坐标.
解答 解:∵OB=CB,OB边上的高CA与OC边上的高BE相交于点D,AB=$\sqrt{2}$,∠CBO=45°,
∴AB=AC=$\sqrt{2}$,OD=CD,∠BOC=$\frac{180°-45°}{2}$=67.5°,
在Rt△BAC中,BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=2,
∴OB=2,
∴OA=OB-AB=2-$\sqrt{2}$,
在Rt△OAC中,OC=$\sqrt{O{A}^{2}+A{C}^{2}}$=2$\sqrt{2-\sqrt{2}}$,
在Rt△OAD中,OA2+AD2=OD2,
(2-$\sqrt{2}$)2+AD2=($\sqrt{2}$-AD)2,
解得:AD=2-$\sqrt{2}$,
∴OA=AD,∠DOA=45°,
∴OD=CD=2$\sqrt{2}$-2,
在Rt△BAD中,BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=2$\sqrt{2-\sqrt{2}}$,
①如图1,△BMC∽△CDO时,过M点作MF⊥AB于F,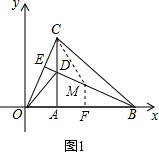
$\frac{BM}{CD}$=$\frac{BC}{CO}$,即$\frac{BM}{2\sqrt{2}-2}$=$\frac{2}{2\sqrt{2-\sqrt{2}}}$,
解得BM=$\sqrt{2\sqrt{2}-2}$,
∵MF⊥AB,CA是OB边上的高,
∴MF∥DA,
∴△BMF∽△BDA,
∴$\frac{BF}{BA}$=$\frac{MF}{DA}$=$\frac{BM}{BD}$,即$\frac{BF}{\sqrt{2}}$=$\frac{MF}{2-\sqrt{2}}$=$\frac{\sqrt{2\sqrt{2}-2}}{2\sqrt{2-\sqrt{2}}}$,
解得BF=1,MF=$\sqrt{2}$-1,
∴OF=OB-BF=1,
∴点M的坐标是(1,$\sqrt{2}$-1);
②如图2,△BCM∽△CDO时,过M点作MF⊥AB于F,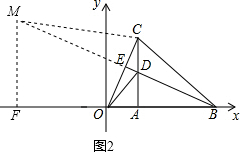
$\frac{BM}{CO}$=$\frac{BC}{CD}$,即$\frac{BM}{2\sqrt{2-\sqrt{2}}}$=$\frac{2}{2\sqrt{2}-2}$,
解得BM=2$\sqrt{2+\sqrt{2}}$,
∵MF⊥AB,CA是OB边上的高,
∴MF∥DA,
∴△BMF∽△BDA,
∴$\frac{BF}{BA}$=$\frac{MF}{DA}$=$\frac{BM}{BD}$,即$\frac{BF}{\sqrt{2}}$=$\frac{MF}{2-\sqrt{2}}$=$\frac{2\sqrt{2+\sqrt{2}}}{2\sqrt{2-\sqrt{2}}}$,
解得BF=2+$\sqrt{2}$,MF=$\sqrt{2}$,
∴OF=BF-OB=$\sqrt{2}$,
∴点M的坐标是(-$\sqrt{2}$,$\sqrt{2}$).
综上所述,点M的坐标是(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$).
故答案为:(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$).
点评 考查了相似三角形的判定与性质,一次函数图象上点的坐标特征,等腰三角形的性质,线段垂直平分线的性质,等腰直角三角形的性质和勾股定理,关键是得到BM的长度,注意分类思想的应用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
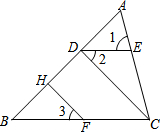 已知,如图,DE∥BC,∠A=60°,∠B=50°;
已知,如图,DE∥BC,∠A=60°,∠B=50°;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;
(1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com