
 (1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;
(1)已知抛物线的顶点为(-1,2),且过点(1,-6),求这个函数的表达式;分析 (1)由于已知抛物线的顶点坐标,则可设顶点式y=a(x+1)2+2,然后把(1,-6)代入求出a的值即可;
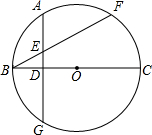
(2)根据垂径定理得$\widehat{AB}$=$\widehat{BC}$,而$\widehat{AB}$=$\widehat{AF}$,则$\widehat{BG}$=$\widehat{AF}$,所以根据圆周角定理得∠1=∠2,然后根据等腰三角形的判定即可得到结论.
解答 (1)解:设抛物线的解析式为y=a(x+1)2+2,
把(1,-6)代入得4a+2=-6,解得a=-2,
所以抛物线的解析式为y=-2(x+1)2+2;
(2)证明: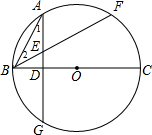 如图,
如图,
∵AG⊥BC,BC为⊙O的直径,
∴$\widehat{AB}$=$\widehat{BC}$,
∵点A是弧BF的中点,
∴$\widehat{AB}$=$\widehat{AF}$,
∴$\widehat{BG}$=$\widehat{AF}$,
∴∠1=∠2,
∴AE=BE.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了圆周角定理.


科目:初中数学 来源: 题型:填空题
 如图所示的数阵叫“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数都为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为$\frac{1}{168}$.
如图所示的数阵叫“莱布尼兹调和三角形”,它是由整数的倒数组成的,第n行有n个数,且两端的数都为$\frac{1}{n}$,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为$\frac{1}{168}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
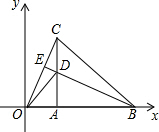 如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=$\sqrt{2}$,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$).
如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=$\sqrt{2}$,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
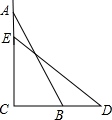 如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米?
如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com