
分析 (1)根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式=3$\sqrt{3}$+1+2-3×$\sqrt{3}$,然后合并即可;
(2)先把括号内通分和除法运算化为乘法运算,然后把分子分母因式分解后约分即可.
解答 解:(1)原式=3$\sqrt{3}$+1+2-3×$\sqrt{3}$
=3;
(2)原式=$\frac{{a}^{2}-4+4}{{a}^{2}-4}$•$\frac{a+2}{a}$
=$\frac{{a}^{2}}{(a+2)(a-2)}$•$\frac{a+2}{a}$
=$\frac{a}{a-2}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了实数的运算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
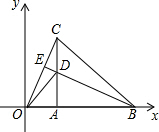 如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=$\sqrt{2}$,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$).
如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=$\sqrt{2}$,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是(1,$\sqrt{2}$-1)或(-$\sqrt{2}$,$\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$ | B. | 3 | C. | -3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com