

分析 (1)根据切线的性质得到CP⊥OC,由于∠OAC=∠AOC=60°,于是得到∠P=90°-∠AOC=30°,在Rt△POC中,求得CO=$\frac{1}{2}$PO=4,即可得到结论;
(2)如图,当S△MAO=S△CAO时,动点M的位置有四种.①作点C关于直径AB的对称点M1,连接AM1,OM1,②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得弧AM的长,即可得到结论.
解答 解:(1)∵CP与⊙O相切,OC是半径.
∴CP⊥OC,
又∵∠OAC=∠AOC=60°,
∴∠P=90°-∠AOC=30°,
∴在Rt△POC中,CO=$\frac{1}{2}$PO=4,
则PO=2CO=8;
(2)如图,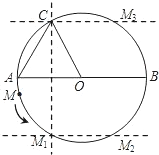
①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得S△M1AO=S△CAO,∠AOM1=60°
∴$\widehat{A{M}_{1}}$
∴当点M运动到M1时,S△MAO=S△CAO,
此时点M经过的弧长为$\frac{60π×4}{180}$=$\frac{4}{3}$π,
∴半径OM所扫过的扇形的面积=$\frac{1}{2}×$$\frac{4}{3}$π×4=$\frac{8}{3}$π;
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO.
∴∠AOM1=∠M1OM2=∠BOM2=60°
∴$\widehat{A{M}_{2}}$=$\frac{4}{3}$π×2或$\widehat{A{M}_{2}}$=$\frac{4π}{180}$×120=$\frac{8}{3}$π,
∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为$\frac{8}{3}$π,
∴半径OM所扫过的扇形的面积=$\frac{1}{2}×\frac{8}{3}$π×4=$\frac{16}{3}$π;
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO=S△CAO
∴∠BOM3=60°,
∴$\widehat{A{M}_{2}{M}_{3}}$=$\frac{4π}{180}×240$或$\widehat{A{M}_{2}{M}_{3}}$=$\frac{8π}{3}$×2=$\frac{16π}{3}$
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为$\frac{16}{3}$π,
∴半径OM所扫过的扇形的面积=$\frac{1}{2}×\frac{16}{3}$π×4=$\frac{32}{3}$π;
④当点M运动到C时,M与C重合,S△MAO=S△CAO,
此时点M经过的弧长为$\frac{4π}{180}$×300°或$\frac{16}{3}$π+$\frac{4}{3}$π=$\frac{20}{3}$π,
∴半径OM所扫过的扇形的面积=$\frac{1}{2}×\frac{20}{3}π$×4=$\frac{40}{3}$π.
点评 本题考查了等边三角形的判定和性质,弧长公式,同底等高的三角形的面积相等的性质扇形的面积的计算,注意分类思想的应用.


科目:初中数学 来源: 题型:解答题
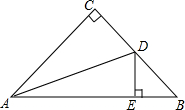 如图,在等腰直角△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E.
如图,在等腰直角△ABC中,∠C=90°,AD平分∠BAC交BC于D,DE⊥AB于E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2ab3的次数是3 | B. | 2x2+3x-1是三次三项式 | ||
| C. | $\frac{1}{3}xy$的系数为$\frac{1}{3}$ | D. | x+1是单项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
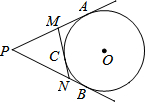 已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )
已知如图,PA、PB切⊙O于A、B,MN切⊙O于C,交PB于N;若PA=7.5cm,则△PMN的周长是( )| A. | 7.5cm | B. | 10cm | C. | 15cm | D. | 12.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2+bx+c,其图象经过A(2,3),B(-2,-5).
已知二次函数y=-x2+bx+c,其图象经过A(2,3),B(-2,-5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com