
| A. | 1 | B. | 无数个 | C. | 0 | D. | 无解 |
分析 分类讨论:x<1,x≥1,根据绝对值的性质,可化简绝对值,根据解一元一次方程的一般步骤,可得答案.
解答 解:①当x<1时,原方程化简得$\frac{1-x}{2}$+$\frac{1-x}{3}$=0,
去分母,得3(1-x)+2(1-x)=0,
去括号,得3-3x+2-2x=0,
移项,得-3x-2x=-3-2,
合并同类项,得-5x=-5,
系数化为1,得x=1(不符合题意的解要舍去);
②当x≥1时,原方程化简得$\frac{x-1}{2}$+$\frac{x-1}{3}$=0,
去分母,得3(x-1)+2(x-1)=0,
去括号,得3x-3+2x-2=0,
移项,得3x+2x=3+2,
合并同类项,得5x=5,
系数化为1,得x=1,
综上所述:x=1是方程的解.
故选:A.
点评 本题考查了含绝对值符号的一元一次方程,利用绝对值的性质化简方程是解题关键,要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:选择题
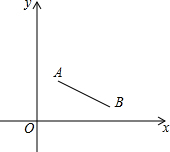 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
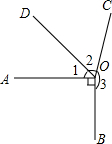 (1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
(1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
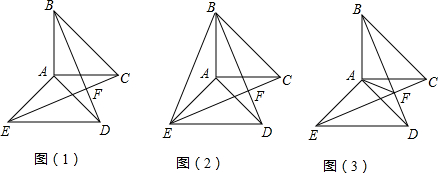
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com