
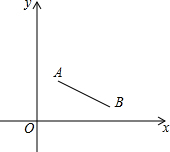
 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
分析 设A1的坐标为(m,n),根据旋转的性质得BA=BA1,∠ABA1=180°,则可判断点B为AA1的中点,根据线段中点坐标公式得到3=$\frac{1+a}{2}$,$\frac{1}{2}$=$\frac{2+b}{2}$,解得a=5,b=-1,然后解方程求出a、b即可得到A1的坐标.
解答 解:设A1的坐标为(m,n),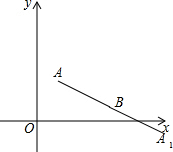
∵线段AB绕点B顺时针旋转180°得线段A1B,
∴BA=BA1,∠ABA1=180°,
∴点B为AA1的中点,
∴3=$\frac{1+a}{2}$,$\frac{1}{2}$=$\frac{2+b}{2}$,解得a=5,b=-1,
∴A1的坐标为(5,-1).
故选C.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.利用线段中点坐标公式是解决本题的关键.


科目:初中数学 来源: 题型:选择题
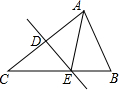 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
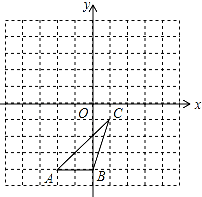 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+$\frac{1}{x}$=1 | B. | ax2+bx+c=0 | C. | x(x-1)=x | D. | x+$\sqrt{x-1}=0$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
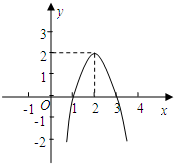 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
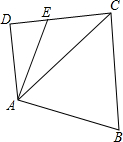 如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$
如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com