
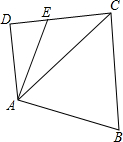
 如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$
如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$分析 (1)作CM⊥AB于M,则∠CMB=∠CMA=90°,求出∠BCM=30°,由含30°角的直角三角形的性质得出BM=$\frac{\sqrt{3}+1}{2}$,求出CM=$\frac{3+\sqrt{3}}{2}$,得出AM,由勾股定理求出AC即可;
(2)由四边形ABCE的面积=△ABC的面积+△ACE的面积,求出AD的长,得出AD=$\frac{1}{2}$AC,即可得出∠ACD=30°.
解答 解:(1)作CM⊥AB于M,如图所示: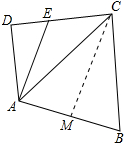
则∠CMB=∠CMA=90°,
∵∠B=60°,
∴∠BCM=30°,
∴BM=$\frac{1}{2}$BC=$\frac{\sqrt{3}+1}{2}$,
∴CM=$\sqrt{3}$BM=$\frac{3+\sqrt{3}}{2}$,AM=AB-BM=2-$\frac{\sqrt{3}+1}{2}$=$\frac{3-\sqrt{3}}{2}$,
∴AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=$\sqrt{(\frac{3-\sqrt{3}}{2})^{2}+(\frac{3+\sqrt{3}}{2}})^{2}$=$\sqrt{6}$;
(2)∵四边形ABCE的面积=△ABC的面积+△ACE的面积=$\frac{3+2\sqrt{3}}{2}$,
即$\frac{1}{2}$×2×$\frac{3+\sqrt{3}}{2}$+$\frac{1}{2}$×$\sqrt{2}$×AD=$\frac{3+2\sqrt{3}}{2}$,
解得:AD=$\frac{\sqrt{6}}{2}$,
∴AD=$\frac{1}{2}$AC,
∵∠D=90°,
∴∠ACD=30°.
点评 本题是面积及等积变换综合题目,考查了含30°角的直角三角形的性质与判定、勾股定理、三角形面积的计算方法等知识点;本题综合性强,有一定难度,特别是(1)中,需要通过作辅助线运用勾股定理才能得出结果.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:选择题
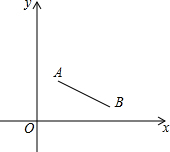 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
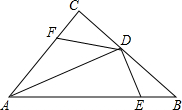 如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.
如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com