
分析 (1)方程利用公式法求出解即可;
(2)方程整理后,利用因式分解法求出解即可;
(3)方程利用平方根定义开方即可求出解.
解答 解:(1)这里a=2,b=-6,c=3,
∵△=36-24=12,
∴x=$\frac{6±2\sqrt{3}}{4}$=$\frac{3±\sqrt{3}}{2}$,
解得:x1=$\frac{3+\sqrt{3}}{2}$,x2=$\frac{3-\sqrt{3}}{2}$;
(2)方程整理得:x2+2x-8=0,即(x-2)(x+4)=0,
解得:x1=2,x2=-4;
(3)开方得:2(2x+1)=3(2x-1)或2(2x+1)=-3(2x-1),
解得:x1=2.5,x2=0.1.
点评 此题考查了解一元二次方程-因式分解法,公式法与直接开平方法,熟练掌握各种解法是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
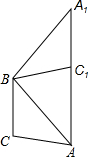 如图,△ACB中,∠BAC=40°,将△ACB绕点B逆时针旋转到△A1C1B,其中点A旋转到点A1,点C旋转到点C1,并且点A、C1、A1三点共线.
如图,△ACB中,∠BAC=40°,将△ACB绕点B逆时针旋转到△A1C1B,其中点A旋转到点A1,点C旋转到点C1,并且点A、C1、A1三点共线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
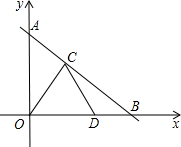 如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.
如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
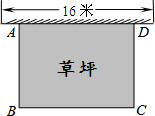 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.则该矩形草坪BC边的长是( )
如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.则该矩形草坪BC边的长是( )| A. | 12 | B. | 18 | C. | 20 | D. | 12或20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
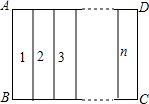 一块矩形绸布的宽AB=a m,长AD=1m,按照图中所示的方式将它裁成相同的n面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即,那么a的值应当是$\frac{\sqrt{n}}{n}$.
一块矩形绸布的宽AB=a m,长AD=1m,按照图中所示的方式将它裁成相同的n面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即,那么a的值应当是$\frac{\sqrt{n}}{n}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com