

分析 (1)1.5分钟后可算出所转的角度,根据半径的长以及构造的直角三角形,可求出答案.
(2)根据所给的高度,能求出OD的长,根据直角三角形中,若直角边是斜边的一半,那么这个直角边所对的角是30°,从而求出转过的∠COD的情况并求解.
(3)从第一次到达10.5m处,到逆时针转到10.5m处,可算出角度,从而可求出时间.
解答 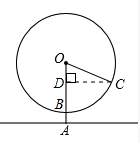 解:(1)∵∠COD=$\frac{1.5}{12}$×360°=45°,OC=20,
解:(1)∵∠COD=$\frac{1.5}{12}$×360°=45°,OC=20,
∴OD=10$\sqrt{2}$,
∴1.5分钟后小美离地面的高度即DA=OA-OD=OB+AB-OD,
=20+0.5-10$\sqrt{2}$≈20.5-10×1.414≈6.4;
故答案为:6.4
(2)∵10.5<OA=20则小美在摩天轮的下半圆,
∵DA=OA-OD,
∴在Rt△ODC中,OD=20.5-10.5=10,OC=20,
∴∠COD=60°,
∴所需时间是$\frac{60}{360}$×12=2分钟,
小美离地面的高度将首次达到10.5m.
(3)∵$\frac{300}{360}$×12=10分钟;
∴10-2=8分钟,连续保持在离地面10.5m以上的空中.
点评 本题考查了解直角三角形的应用、生活中的旋转现象,关键是看到转过的角度和时间的关系,以及对两种情况的考虑,千万不能漏解.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:填空题
 在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,回答问题:
在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,阅读下列材料,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
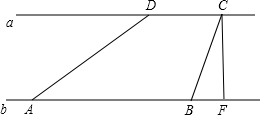 如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,河流两岸a、b平行,C、D是河岸a上间隔50米的两根电线杆,某人在河岸b上的A处测得∠DAE=30°,然后沿河岸走了100米到达B处,测得∠CBF=60°,则河流的宽度CF的值为43m(结果精确到个位,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
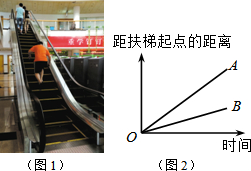 大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )| A. | 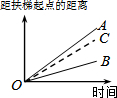 | B. | 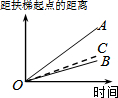 | C. | 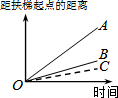 | D. | 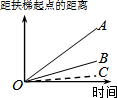 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com