
【题目】平面直角坐标系中,A是y=﹣![]() (x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____.
(x>0)图象上一点,B是x轴正半轴上一点,点C的坐标为(0,﹣2),若点D与A,B,C构成的四边形为正方形,则点D的坐标_____.
【答案】(4,﹣2)或(2,﹣4)或(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).
【解析】
首先依据题意画图图形,对于图1和图2依据正方形的对称性可得到点D的坐标,对于图3可证明△AEC≌△BFA,从而可得到AE=BF,然后由反比例函数的解析式可求得点A的坐标,然后可得到点D的坐标.
如图1所示:当CD为对角线时.
∵OC=2,AB=CD=4,
∴D(4,﹣2).
如图2所示:
∵OC=2,BD=AC=4,
∴D(2,﹣4).
如图3所示:过点A作AE⊥y轴,BF⊥AE,则△AEC≌△BFA.
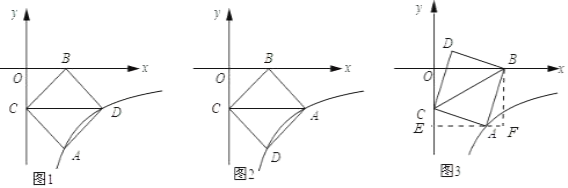
∴AE=BF.
设点A的横纵坐标互为相反数,
∴A(2![]() ,﹣2
,﹣2![]() )
)
∴D(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).
综上所述,点D的坐标为(4,﹣2)或(2,﹣4)或(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).
故答案为:(4,﹣2)或(2,﹣4)或(2![]() ﹣2,2
﹣2,2![]() ﹣2).
﹣2).


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】下图的数阵由88个偶数排成.现用一个如图所示的平行四边形框可以框出四个数;
①图中平行四边形框内的四个数有什么关系?
②在数阵中任意作一类似(1)中的平行四边形框,设其中左上角的一个数是![]() ,那么其他三个数怎样表示?
,那么其他三个数怎样表示?
③在这个数阵的平行四边形框内,是否存在和为288的四个数?若存在,求出这四个数;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )

A.CE=![]() DE B.CE=
DE B.CE=![]() DE C.CE=3DE D.CE=2DE
DE C.CE=3DE D.CE=2DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两盒中各有3张卡片,卡片上分别标有数字﹣7、﹣1、3和﹣2、1、6,这些卡片除数字外都相同.把卡片洗匀后,从甲、乙两盒中各任意抽取1张,并把抽得卡片上的数字分别作为平面直角坐标系中一个点的横坐标、纵坐标.
(1)列出这样的点所有可能的坐标;
(2)求这些点落在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
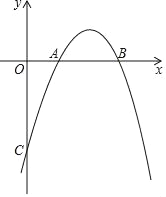
【题目】己知,二次函数y=﹣x2+bx+c的图象与x轴的两个交点A,B的横坐标分别为1和2,与y轴的交点是C.
(1)求这个二次函数的表达式;
(2)若点D是y轴上的一点,是否存在D,使以B,C,D为顶点的三角形与△ABC相似?若存在,求点D的坐标,若不存在,请说明理由;
(3)过点C作CE∥x轴,与二次函数y=﹣x2+bx+c的图象相交于点E,点H是该二次函数图象上的动点,过点H作HF∥y轴,交线段BC于点F,试探究当点H运动到何处时,△CHF与△HFE的面积之和最大,求点H的坐标及最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图像与反比例函数![]() (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,有下列说法:①甲、乙同学都骑行了18km;②甲、乙同学同时到达B地;③甲停留前、后的骑行速度相同;④乙的骑行速度是![]() ;其中正确的说法是( )
;其中正确的说法是( )
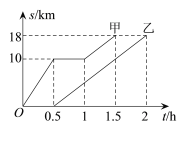
A. ①③B. ①④C. ②④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据
月份n(月)1 | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com