
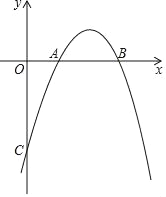
����Ŀ����֪�����κ���y=��x2+bx+c��ͼ����x�����������A��B�ĺ�����ֱ�Ϊ1��2����y��Ľ�����C��
��1����������κ����ı���ʽ��
��2������D��y���ϵ�һ�㣬�Ƿ����D��ʹ��B��C��DΪ���������������ABC���ƣ������ڣ����D�����꣬�������ڣ���˵�����ɣ�
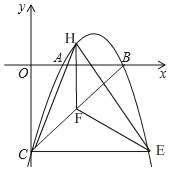
��3������C��CE��x�ᣬ����κ���y=��x2+bx+c��ͼ���ཻ�ڵ�E����H�Ǹö��κ���ͼ���ϵĶ��㣬����H��HF��y�ᣬ���߶�BC�ڵ�F����̽������H�˶����δ�ʱ����CHF����HFE�����֮��������H�����꼰��������
���𰸡���1�����κ����ı���ʽy=��x2+3x��2����2��D��0����1����D��0��6������3��������Ϊ1.5��H��1��0����
�������������������1������֪���ô���ϵ����������⼴�ɵý���ʽ��
��2��������������������������εı���ʽ���������D�����ꣻ
��3�������ֱ��BC�Ľ���ʽ�����������CHF���HFE�����֮�͵ĺ�����ϵʽ������������ֵ.
�����������1���߶��κ���y=��x2+bx+c��ͼ����x�����������A��B�ĺ�����ֱ�Ϊ1��2��
��A��1��0����B��2��0����
��![]() ��
��
��![]() ��
��
����κ����ı���ʽy=��x2+3x��2��
��2���߶��κ����ı���ʽy=��x2+3x��2��
��C��0����2����
��OC=2��
��A��1��0����B��2��0��
��OB=2��
��OB=OC��
���OBC=��OCB=45�㣬
���BAC��135�㣬������Dֻ���ڵ�C�Ϸ���y���ϣ�
���DCB=��ABC=45��
����D��0��d����d����2��
��A��1��0����B��2��0����C��0����2����
��AB=1��BC=2![]() ��CD=d+2��
��CD=d+2��
����B��C��DΪ��������������ABC���ƣ�
��١�DCB�ס�ABC��
��![]() =1��
=1��
��CD=AB=1��
��d+2=1��
��d=��1��
��D��0����1����
�ڡ�BCD�ס�ABC��
��![]() ��
��
��![]() ��
��
��d=6��
��D��0��6����
��3����ͼ��
��CE���ᣬ
����y=��2��
�ੁ2=��x2+3x��2��
��x=0���ᣩ��x=3��
��E��3����2����
��B��2��0����C��0����2����
��ֱ��BC�Ľ���ʽΪy=x��2����H��m����m2+3m��2����F��m��m��2����
�ߵ�F���߶�BC�ϵĵ㣬
��0��m��2��HF=��m2+3m��2����m��2��=��m2+2m��
��S��CHF+S��EHF=![]() HF��3=
HF��3=![]() ����m2+2m��=��
����m2+2m��=��![]() ��m2��2m+1��+
��m2��2m+1��+![]() =��
=��![]() ��m��1��2+
��m��1��2+![]() ��
��
��m=1ʱ����CHF���HFE�����֮�����������Ϊ![]() ����ʱ��H��1��0����
����ʱ��H��1��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬������
���е㣬������![]() ��1
��1![]() ���ٶȴ�
���ٶȴ�![]() �����������
�����������![]() �ķ����˶�����
�ķ����˶�����![]() ����˶�ʱ��Ϊ
����˶�ʱ��Ϊ![]() �루
�루![]() ��������
��������![]() ����
����![]() ��ֱ��������ʱ��
��ֱ��������ʱ��![]() ��ֵΪ_____��
��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
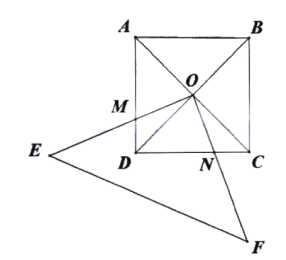
����Ŀ����ͼ����֪��ABC�У�AB��AC���ѡ�ABC��A����˳ʱ�뷽����ת�õ���ADE������BD��CE���ڵ�F.
(1)��֤����AEC�ա�ADB��
(2)��AB��2����BAC��45�㣬���ı���ADFC������ʱ����BF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й���һԪ���η���x2+bx+c��0���ĸ�����
�ٵ�c��0��b��0ʱ���������һ������������ȵ�ʵ������
�ڵ�c��0ʱ����p�Ƿ���x2+bx+c��0��һ��������![]() �Ƿ���cx2+bx+1��0��һ������
�Ƿ���cx2+bx+1��0��һ������
����c��0����һ����������ʵ��m��n��ʹ��m2+mb+c��0��n2+nb+c��
����p��q�Ƿ��̵�����ʵ��������p��q��![]() ��
��
�����Ǽ����������ǣ�������
A. ��B. ��C. ��D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У�A��y����![]() ��x��0��ͼ����һ�㣬B��x����������һ�㣬��C������Ϊ��0����2��������D��A��B��C���ɵ��ı���Ϊ�����Σ����D������_____��
��x��0��ͼ����һ�㣬B��x����������һ�㣬��C������Ϊ��0����2��������D��A��B��C���ɵ��ı���Ϊ�����Σ����D������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ƽ���ı���ֽƬABCD��Ҫ��������ѧ֪ʶ�������һ�����Σ��ס�����λͬѧ�������ֱ����£�
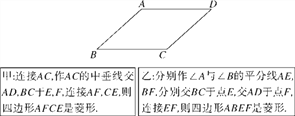
���ڼס������˵����������ж�(����)
A. ����ȷ���Ҵ��� B. �״�������ȷ
C. �ס��Ҿ���ȷ D. �ס��Ҿ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
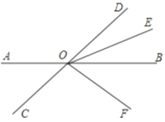
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OEƽ�֡�BOD��OFƽ�֡�COE����BOF=30�������BOE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͳ��ͼ��ӳ���ҹ��ʵ�ҵ������ҵ�������ҵ�������������
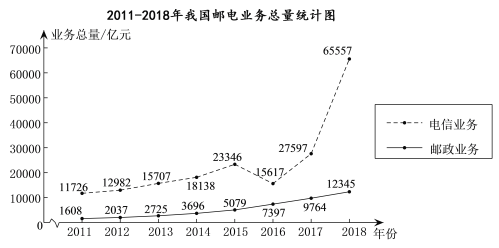
������������Դ�ڹ���ͳ�ƾ֣�
����ͳ��ͼ�ṩ����Ϣ�������й��ҹ��ʵ�ҵ�������ƶ����������ǣ� ��
A. 2018�꣬����ҵ������������ҵ��������5������
B. 2011��2018�꣬����ҵ�����������ҵ��������������������
C. ��2017����ȣ�2018������ҵ�������������ʳ���20%
D. 2011��2018�꣬����ҵ��������������ƽ��ֵ��������ҵ��������������ƽ��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ĶԽ���
�ĶԽ���![]() ���ڵ�
���ڵ�![]() ��ֱ��������
��ֱ��������![]() �Ƶ�
�Ƶ�![]() ����ʱ����ת��
����ʱ����ת��![]()
��1����ֱ���������Ƶ�![]() ��ʱ��ת�������зֱ�
��ʱ��ת�������зֱ�![]() ������
������![]() ����
����
����֤��![]() ��
��
������![]() ����ô
����ô![]() ��ʲô���Ĺ�ϵ����˵������
��ʲô���Ĺ�ϵ����˵������
��2���������εı߳�Ϊ2����������![]() ��
��![]() ����ͼ���ص����ֵ����Ϊ���٣�������д����ֱ��д�������
����ͼ���ص����ֵ����Ϊ���٣�������д����ֱ��д�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com