
【题目】下列关于一元二次方程x2+bx+c=0的四个命题
①当c=0,b≠0时,这个方程一定有两个不相等的实数根;
②当c≠0时,若p是方程x2+bx+c=0的一个根,则![]() 是方程cx2+bx+1=0的一个根;
是方程cx2+bx+1=0的一个根;
③若c<0,则一定存在两个实数m<n,使得m2+mb+c<0<n2+nb+c;
④若p,q是方程的两个实数根,则p﹣q=![]() ,
,
其中是假命题的序号是( )
A. ①B. ②C. ③D. ④
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ,∠CON= ;
(3)若∠BOC=α,∠NOC=β,将三角板MON绕点O逆时针旋转至图③时,求∠AOM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表). 设一个月内使用移动电话主叫的时间为t分钟
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 58元 | 150分钟 | 0.25元/分 | 免费 |
方式二 | 88元 | 350分钟 | 0.19元/分 | 免费 |

(t为正整数),请根据表中提供的信息回答下列问题:
(1)方式一中,当t超过150分钟时,该月费用表示为: 元(用含t的代数式表示);方式二中,当t超过350分钟时,该月费用表示为: 元(用含t的代数式表示).
(2)当t=300时,哪种计费方式的费用较省?请作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )

A.CE=![]() DE B.CE=
DE B.CE=![]() DE C.CE=3DE D.CE=2DE
DE C.CE=3DE D.CE=2DE
查看答案和解析>>
科目:初中数学 来源: 题型:
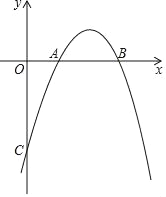
【题目】己知,二次函数y=﹣x2+bx+c的图象与x轴的两个交点A,B的横坐标分别为1和2,与y轴的交点是C.
(1)求这个二次函数的表达式;
(2)若点D是y轴上的一点,是否存在D,使以B,C,D为顶点的三角形与△ABC相似?若存在,求点D的坐标,若不存在,请说明理由;
(3)过点C作CE∥x轴,与二次函数y=﹣x2+bx+c的图象相交于点E,点H是该二次函数图象上的动点,过点H作HF∥y轴,交线段BC于点F,试探究当点H运动到何处时,△CHF与△HFE的面积之和最大,求点H的坐标及最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.
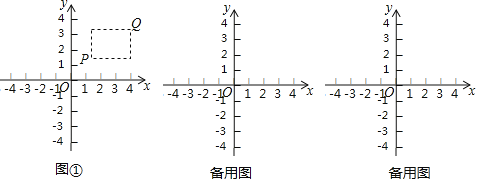
已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com