
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ,∠CON= ;
(3)若∠BOC=α,∠NOC=β,将三角板MON绕点O逆时针旋转至图③时,求∠AOM.

【答案】(1)25°;(2)40°,25°;(3)∠AOM=90°﹣(α+β).
【解析】
(1)根据∠MOC=∠MON﹣∠BOC代入数据计算即可得解;
(2)根据角平分线的定义可得∠MOB=2∠BOC,再根据旋转角∠BON=∠MOB﹣∠MON计算即可得解,然后根据∠CON=∠BOC﹣∠BON计算;
(3)先求出∠BON,再根据∠AOM=∠AOB﹣∠MON﹣∠BON代入数据计算即可得解.
解:(1)∠MOC=∠MON﹣∠BOC,
=90°﹣65°,
=25°;
(2)∵OC是∠MOB的角平分线,
∴∠MOB=2∠BOC=2×65°=130°,
∴旋转角∠BON=∠MOB﹣∠MON,
=130°﹣90°,
=40°,
∠CON=∠BOC﹣∠BON,
=65°﹣40°,
=25°;
(3)∵∠BOC=α,∠NOC=β,
∴∠BON=∠NOC+∠BOC=α+β,
∵点O为直线AB上一点,
∴∠AOB=180°,
∵∠MON=90°,
∴∠AOM=∠AOB﹣∠MON﹣∠BON,
=180°﹣90°﹣(α+β),
=90°﹣(α+β).
故答案为:(1)25°;(2)40°,25°;(3)∠AOM=90°﹣(α+β).


科目:初中数学 来源: 题型:
【题目】如图,AB=4,动点P从A出发,在直线AB上以每秒3个单位的速度向右运动,到达B后立即返回,回到A后停止运动,动点Q与P同时从A出发,在直线AB上以每秒1个单位的速度向左运动,当P停止运动时,点Q也停止运动,设点P的运动时间为t秒.
![]()
(1)若t=1,则BP的长是 PQ的长是 .
(2)当点P回到点A时,求BQ的长.
(3)在直线AB上取点C,使B是线段PC的中点,在点P的整个运动过程中,是否存在AC=AQ+3,若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浏阳河风光带位于湖南省长沙市芙蓉区浏阳河西岸,是人们休闲的好去处.如图,是一幅简易的风光带地图,点![]() 为一游客休息处.我们可把风光带看作一条弯曲的数轴,点
为一游客休息处.我们可把风光带看作一条弯曲的数轴,点![]() 作为原点,点
作为原点,点![]() 、
、![]() 、
、![]() 是风光带上顺次三点,从点
是风光带上顺次三点,从点![]() 往点
往点![]() 的方向记作正方向,点
的方向记作正方向,点![]() 、
、![]() 之间的路程记为
之间的路程记为![]() ,点
,点![]() 、
、![]() 之间的路程记为
之间的路程记为![]() ,开始时
,开始时![]() 点表示的数为
点表示的数为![]() ,
,![]() 点表示的数为
点表示的数为![]() (单位:米).
(单位:米).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)在(1)的条件下,有甲、乙、丙游客三位分别从点![]() 、
、![]() 、
、![]() 的初始位置同时出发开始沿风光带运动,其中甲以每分钟
的初始位置同时出发开始沿风光带运动,其中甲以每分钟![]() 米的速度向负方向运动,乙、丙分别以每分钟
米的速度向负方向运动,乙、丙分别以每分钟![]() 米和
米和![]() 米的速度沿风光带向正方向运动.求运动多少分钟后,乙、丙之间的路程与甲、乙之间的路程相等.
米的速度沿风光带向正方向运动.求运动多少分钟后,乙、丙之间的路程与甲、乙之间的路程相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果![]() (
(![]() ,
,![]() 为正数),那么我们把
为正数),那么我们把![]() 叫做
叫做![]() 的
的![]() 数,记作
数,记作![]() .
.
(1)根据![]() 数的定义,填空:
数的定义,填空:![]() ____________;
____________;![]() ____________.
____________.
(2)![]() 数有如下运算性质:
数有如下运算性质:![]() ,
,![]() .根据运算性质,计算:
.根据运算性质,计算:
①若![]() ,求
,求![]() ;
;
②若![]() ,
,![]() ,求
,求![]() .
.
(3)若设![]() ,
,![]() ,则下列算式中错误的是________(直接填序号).
,则下列算式中错误的是________(直接填序号).
①![]() ②
②![]() ③
③![]()
④![]() ⑤
⑤![]() ⑥
⑥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
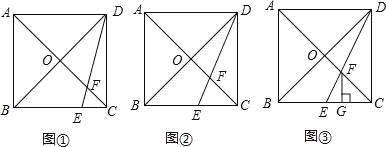
【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE, 交 AC于点F.
(1)如图①,当![]() 时,求
时,求![]() 的值;
的值;
(2)如图②当DE平分∠CDB时,求证:AF=![]() OA;
OA;
(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=![]() BG.
BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分). 小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.
(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为____ cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是_____cm.
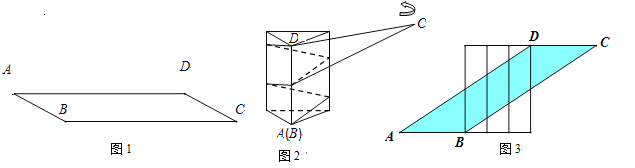
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于一元二次方程x2+bx+c=0的四个命题
①当c=0,b≠0时,这个方程一定有两个不相等的实数根;
②当c≠0时,若p是方程x2+bx+c=0的一个根,则![]() 是方程cx2+bx+1=0的一个根;
是方程cx2+bx+1=0的一个根;
③若c<0,则一定存在两个实数m<n,使得m2+mb+c<0<n2+nb+c;
④若p,q是方程的两个实数根,则p﹣q=![]() ,
,
其中是假命题的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com