
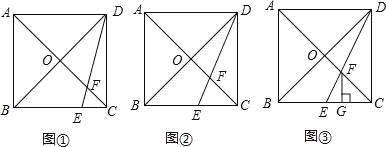
【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE, 交 AC于点F.
(1)如图①,当![]() 时,求
时,求![]() 的值;
的值;
(2)如图②当DE平分∠CDB时,求证:AF=![]() OA;
OA;
(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=![]() BG.
BG.
【答案】(1)![]() ;(2)(3)见解析
;(2)(3)见解析
【解析】试题分析:(1)利用相似三角形的性质求得![]() 与
与![]() 的比值,依据
的比值,依据![]() 和
和![]() 同高,则面积的比就是
同高,则面积的比就是![]() 与
与![]() 的比值,据此即可求解;
的比值,据此即可求解;
(2)利用三角形的外角和定理证得![]() 可以证得
可以证得![]() ,在直角
,在直角![]() 中,利用勾股定理可以证得;
中,利用勾股定理可以证得;
(3)连接![]() 易证
易证![]() 是
是![]() 的中位线,然后根据
的中位线,然后根据![]() 是等腰直角三角形,易证
是等腰直角三角形,易证![]() 利用相似三角形的对应边的比相等即可.
利用相似三角形的对应边的比相等即可.
试题解析:(1)∵![]() ,∴
,∴![]()
![]()
∵四边形ABCD是正方形,
![]()
∴△CEF∽△ADF,∴![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
(2)证明:∵DE平分∠CDB,
∴∠ODF=∠CDF,
∵AC、BD是正方形ABCD的对角线。
![]()
而∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,
∴∠ADF=∠AFD,
∴AD=AF,
在![]() 中,根据勾股定理得:
中,根据勾股定理得:
![]() =
=![]() OA,
OA,
![]()
(3)证明:连接OE.
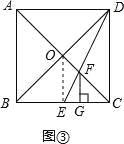
∵点O是正方形ABCD的对角线AC、BD的交点,
点O是BD的中点。
又∵点E是BC的中点,
∴OE是△BCD的中位线,
![]()
![]()
∴![]() =
=![]() ,∴
,∴![]() .
.
![]()
![]()
.在![]() 中,∵∠GCF=45°.∴CG=GF,
中,∵∠GCF=45°.∴CG=GF,
又∵CD=BC,∴![]() ,
,
∴![]() =
=![]() .
.
∴CG![]() =BG.
=BG.


科目:初中数学 来源: 题型:
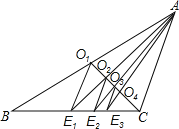
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn= AC.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
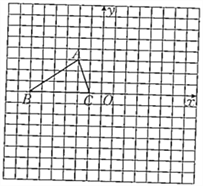
【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)画出将△ABC绕坐标原点O逆时针旋转90°图形.
(2)填空:以A、B、C为顶点的平行四边形的第四个顶点D的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(选做题)包括两个小题,请选定其中一个小题用一元一次方程作答.
A.一根尼龙绳,小江第一次用去它的一半少![]() 米,第二次用去
米,第二次用去![]() 米,结果还剩下原来的
米,结果还剩下原来的![]() ,试问这根尼龙绳原来有多长?
,试问这根尼龙绳原来有多长?
B.小苏、小江家相距![]() 千米且附近均设有火车站,一列慢车从小江家附近的火车站驶往小苏家附近的火车站,速度为
千米且附近均设有火车站,一列慢车从小江家附近的火车站驶往小苏家附近的火车站,速度为![]()
![]() ,一列快车从小苏家附近的火车站驶往小江家附近的火车站,速度为
,一列快车从小苏家附近的火车站驶往小江家附近的火车站,速度为![]()
![]() ,若两车同时出发,多少时间后两车相距
,若两车同时出发,多少时间后两车相距![]()
![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小兵、小英三人的家和学校在同一条东西走向的大街上,星期天班主任到这三位学生家进行家访,班主任从学校出发先向东走0.5千米到小明家,后又向东走1.5千米到小兵家,再向西走5千米到小英家,最后回到学校。
(1)以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小英三人家的位置。
(2)小明家距离小英家多远?
(3)这次家访,班主任共走了多少千米路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,∠BOC=30°,C在∠AOB外部,OM平分∠AOC,ON平分∠BOC. 则∠MON= 度.
(1)若∠AOB=α,其他条件不变,则∠MON= 度.
(2)若∠BOC=β(β为锐角),其他条件不变,则∠MON= 度.
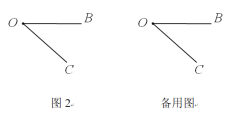
(3)若∠AOB=α且∠BOC=β(β为锐角),求∠MON的度数(请在图2中画出示意图并解答)
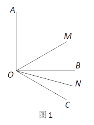
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
+11 | +10 | ﹣17 | +18 | ﹣12 |
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
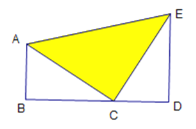
【题目】如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.
(1)求△ABC的周长;
(2)求△ACE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com