
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.
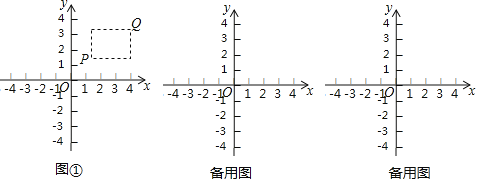
已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
【答案】(1)2;(2)若点A,C的“相关矩形”为正方形,直线AC的表达式为y=x-1或y=-x+1;(3)b>0或b<-8.
【解析】
(1)由相关矩形的定义可知:要求A与B的相关矩形面积,则AB必为对角线,利用A、B两点的坐标即可求出该矩形的底与高的长度,进而可求出该矩形的面积;
(2)由定义可知,AC必为正方形的对角线,所以AC与x轴的夹角必为45,设直线AC的解析式为;y=kx+b,由此可知k=±1,再(1,0)代入y=kx+b,即可求出b的值;
(3)分别把点A、D点的坐标代入y=2x+b±2,求得b的数值即可.
(1)∵A(1,0),B(3,1)
由定义可知:点A,B的“相关矩形”的底与高分别为2和1,
∴点A,B的“相关矩形”的面积为2×1=2;
(2)由定义可知:AC是点A,C的“相关矩形”的对角线,
又∵点A,C的“相关矩形”为正方形
∴直线AC与x轴的夹角为45°,
设直线AC的解析为:y=x+m或y=-x+n
把(1,0)代入y=x+m,
∴m=-1,
∴直线AC的解析为:y=x-1,
把(1,0)代入y=-x+n,
∴n=1,
∴y=-x+1,
综上所述,若点A,C的“相关矩形”为正方形,直线AC的表达式为y=x-1或y=-x+1;
(3)把A(1,0),D(4,2)分别代入y=2x+b±2,
得出b=0,或b=-8,
∴b>0或b<-8


科目:初中数学 来源: 题型:
【题目】下列关于一元二次方程x2+bx+c=0的四个命题
①当c=0,b≠0时,这个方程一定有两个不相等的实数根;
②当c≠0时,若p是方程x2+bx+c=0的一个根,则![]() 是方程cx2+bx+1=0的一个根;
是方程cx2+bx+1=0的一个根;
③若c<0,则一定存在两个实数m<n,使得m2+mb+c<0<n2+nb+c;
④若p,q是方程的两个实数根,则p﹣q=![]() ,
,
其中是假命题的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图反映了我国邮电业务(含邮政业务与电信业务)总量的情况.
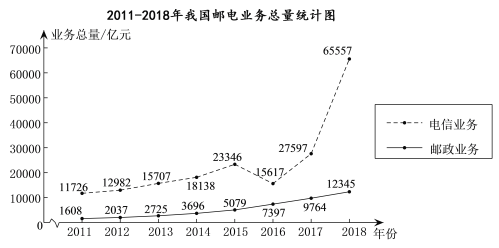
(以上数据来源于国家统计局)
根据统计图提供的信息,下列有关我国邮电业务总量推断不合理的是( )
A. 2018年,电信业务总量比邮政业务总量的5倍还多
B. 2011—2018年,邮政业务总量与电信业务总量都是逐年增长的
C. 与2017年相比,2018年邮政业务总量的增长率超过20%
D. 2011—2018年,电信业务总量年增长的平均值大于邮政业务总量年增长的平均值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)整式加减
①6a2b+5ab2﹣4ab2﹣7a2b
②5a2b﹣[2a2b﹣(ab2﹣2a2b)﹣4]﹣2ab2
(2)先化简,再求值
①5a2+3b2+2(a2﹣b2)﹣(52﹣3b2),其中a=﹣1,b=![]() .
.
②2(xy2+xy)﹣3(xy2﹣yx)﹣4yx2,其中|x+1|+(y﹣1)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ac>0;②当x>1时,函数y随x的增大而增大;③a+b+c=0;④2a+b=0;⑤当y>0时,﹣1<x<3.其中,正确的说法有( )个
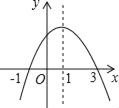
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶12千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.
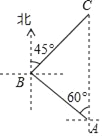
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,直角三角形
,直角三角形![]() 绕点
绕点![]() 按逆时针旋转,
按逆时针旋转,![]()
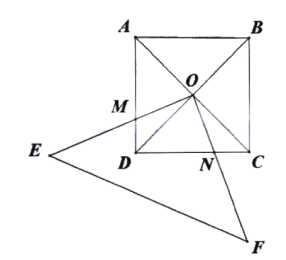
(1)若直角三角形绕点![]() 逆时针转动过程中分别交
逆时针转动过程中分别交![]() 两边于
两边于![]() 两点
两点
①求证:![]() ;
;
②连接![]() ,那么
,那么![]() 有什么样的关系?试说明理由
有什么样的关系?试说明理由
(2)若正方形的边长为2,则正方形![]() 与
与![]() 两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
两个图形重叠部分的面积为多少?(不需写过程直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当![]() 时,在数轴上数
时,在数轴上数![]() 和数
和数![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,若点
,若点![]() 表示的数分别为
表示的数分别为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]()

(1)在图中标出三点的位置
![]()
![]() ;
;![]() .
.
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和
和![]() 点分别以每秒
点分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动.
个单位长度的速度向右运动.
试问:①![]() 秒后点
秒后点![]() 表示的数为 .
表示的数为 .
②![]() 的值是否随着运动时间
的值是否随着运动时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD的边长为5,∠DAB=60°.将菱形ABCD绕着A逆时针旋转得到菱形AEFG,设∠EAB=α,且0°<α<90°,连接DG、BE、CE、CF.
(1)如图(1),求证:△AGD≌△AEB;
(2)当α=60°时,在图(2)中画出图形并求出线段CF的长;
(3)若∠CEF=90°,在图(3)中画出图形并求出△CEF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com