
【题目】已知菱形ABCD的边长为5,∠DAB=60°.将菱形ABCD绕着A逆时针旋转得到菱形AEFG,设∠EAB=α,且0°<α<90°,连接DG、BE、CE、CF.
(1)如图(1),求证:△AGD≌△AEB;
(2)当α=60°时,在图(2)中画出图形并求出线段CF的长;
(3)若∠CEF=90°,在图(3)中画出图形并求出△CEF的面积.

【答案】(1)见解析;(2)5![]() ;(3)
;(3)![]()
【解析】试题分析:(1)利用AD=AB,AG=AE,∠GAD=∠EAB(SAS)证明△AGD≌△AEB即可;
(2)当α=60°时,AE与AD重合,作DH⊥CF于H.由已知可得∠CDF=120°,DF=DC=5.在Rt△CDH中,CH=DCsin60°,继而求出CF的长;
(3)当∠CEF=90°时,延长CE交AG于M,连接AC,∠CEF=90°,只需求出EC的长,又EC=MC﹣ME.在Rt△AME和Rt△AMC中求解MC和ME的长即可.
试题解析:解:(1)∵菱形ABCD绕着点A逆时针旋转得到菱形AEFG,∴AG=AD,AE=AB,∠GAD=∠EAB=α.∵四边形AEFG是菱形,∴AD=AB,∴AG=AE,∴△AGD≌△AEB.
(2)解法一:如图(1),当α=60°时,AE与AD重合,作DH⊥CF于H.由已知可得∠CDF=120°,DF=DC=5,∴∠CDH=![]() ∠CDF=60°,CH=
∠CDF=60°,CH=![]() CF.
CF.
在Rt△CDH中,∵CH=DCsin60°=5×![]() =
=![]() ,∴CF=2CH=5
,∴CF=2CH=5![]() .
.
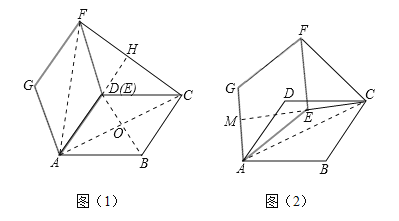
解法二:如图(1),当α=60°时,AE与AD重合,连接AF、AC、BD、AC与BD交于点O.
由题意,知AF=AC,∠FAC=60°,∴△AFC是等边三角形,∴FC=AC.
由已知,∠DAO=![]() ∠BAD=30°,AC⊥BD,∴AO=ADcos30°=
∠BAD=30°,AC⊥BD,∴AO=ADcos30°=![]() ,∴AC=2AO=5
,∴AC=2AO=5![]() ,∴FC=AC=5
,∴FC=AC=5![]() .
.
(3)如图(2),当∠CEF=90°时,延长CE交AG于M,连接AC.
∵四边形AEFG是菱形,∴EF∥AG.
∵∠CEF=90°,∴∠GME=90°,∴∠AME=90°.
在Rt△AME中,AE=5,∠MAE=60°,∴AM=AEcos60°=![]() ,EM=AEsin60°=
,EM=AEsin60°=![]() .
.
在Rt△AMC中,易求AC=5![]() ,∴MC=
,∴MC=![]() =
=![]() ,∴EC=MC﹣ME=
,∴EC=MC﹣ME=![]() ﹣
﹣![]() (
(![]() ﹣
﹣![]() ),∴S△CEF=
),∴S△CEF=![]() ECEF=
ECEF=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.
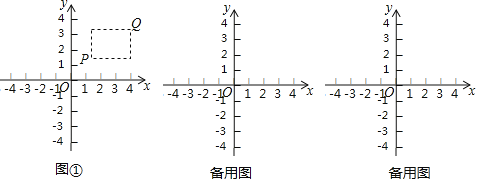
已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后, ![]() 能被x0+3整除,…,
能被x0+3整除,…, ![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于每个正整数 n,关于 x 的一元二次方程![]() 0 的两个根分别为 an、bn,设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an,0),Bn(bn,0),AnBn 表示这两点间的距离,则 AnBn=____________(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为______.
0 的两个根分别为 an、bn,设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an,0),Bn(bn,0),AnBn 表示这两点间的距离,则 AnBn=____________(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
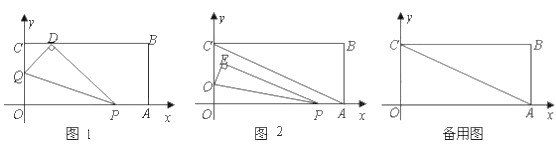
【题目】将一矩形纸片OABC 放在平面直角坐标系中, O(0,0) , A(6,0) , C(0,3) .动点Q 从点O 出发以每秒 1 个单位长的速度沿OC 向终点C 运动,运动![]() 秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
(1)用含t 的代数式表示OP,OQ ;
(2)当t 1时,如图 1,将△OPQ 沿 PQ 翻折,点O 恰好落在CB 边上的点 D 处,求点 D 的坐标;
(3)连结 AC ,将△OPQ 沿 PQ 翻折,得到△EPQ ,如图 2.问: PQ 与 AC 能否平行? PE 与 AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
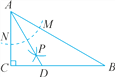
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC∶S△ABC=1∶3.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
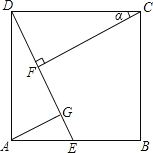
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在结束了380课时初中阶段教学内容的教学后,刘老师计划在增加60课时用于总复习,将380课时按内容所占比例,绘制如下统计图表(图1和~图2),请根据图表提供的信息,回答下列问题:

(1)图1中“统计与概率”所在扇形的圆心角为度;
(2)图2中的a= ;
(3)在60课时的总复习中,刘老师应安排多少课时复习“数与代数”内容?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“手机使用目的”和“每周使用手机时间”的问卷调查,并绘制成如图①②的统计图。已知“查资料”人人数是40人。
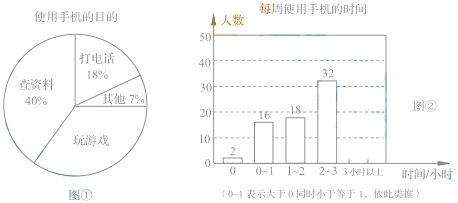
请你根据以上信息解答以下问题
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是_______________。
(2)补全条形统计图
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com