
【题目】将一矩形纸片OABC 放在平面直角坐标系中, O(0,0) , A(6,0) , C(0,3) .动点Q 从点O 出发以每秒 1 个单位长的速度沿OC 向终点C 运动,运动![]() 秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
(1)用含t 的代数式表示OP,OQ ;
(2)当t 1时,如图 1,将△OPQ 沿 PQ 翻折,点O 恰好落在CB 边上的点 D 处,求点 D 的坐标;
(3)连结 AC ,将△OPQ 沿 PQ 翻折,得到△EPQ ,如图 2.问: PQ 与 AC 能否平行? PE 与 AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.
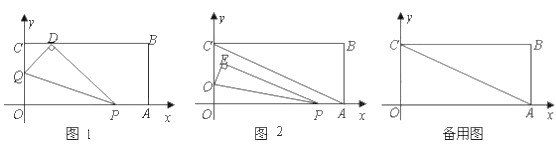
【答案】(1) OP 6 t , OQ t ![]() (2)D(1,3);(3)① PQ 能与 AC 平行,t
(2)D(1,3);(3)① PQ 能与 AC 平行,t ![]() ,② PE 不能与 AC 垂直,理由见解析.
,② PE 不能与 AC 垂直,理由见解析.
【解析】
(1)由O(0,0),A(6,0),C(0,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据P点与Q点的运动速度与运动时间即可用含t的代数式表示OP,OQ;
(2)由翻折的性质可知:△OPQ≌△DPQ,进而可得:DQ=OQ,然后由t=1时,DQ=OQ=![]() ,CQ=OCOQ=
,CQ=OCOQ=![]() ,然后利用勾股定理可求CD的值,进而可求点D的坐标;
,然后利用勾股定理可求CD的值,进而可求点D的坐标;
(3)① PQ 能与 AC 平行。若 PQ ∥ AC ,得到![]() ,t
,t ![]() ;② PE 不能与 AC 垂直。若 PE AC ,延长QE 交OA 于 F,得到
;② PE 不能与 AC 垂直。若 PE AC ,延长QE 交OA 于 F,得到![]() ,t 3.45 ,即可解答
,t 3.45 ,即可解答
(1)∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点Q从O点以每秒1个单位长的速度沿OC向终点C运动,运动23秒时,动点P从点A出发以相等的速度沿AO向终点O运动.
∴当点P的运动时间为t(秒)时,
AP=t,OQ t ![]() ,
,
则OP=OAAP=6t;
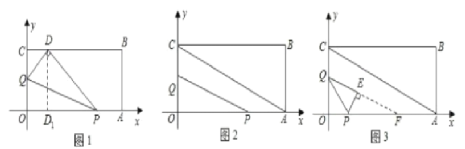
(2)当t 1时,过 D 点作 DD1 OA ,交OA 于 D1 ,如图 1,
则 DQ QO=![]() , QC
, QC ![]() ,
,
CD 1 , D(1,3)
(3)① PQ 能与 AC 平行.若 PQ ∥ AC ,如图 2,
则![]() ,
,
即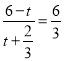 ,
,
t ![]() ,而0 ≤ t ≤
,而0 ≤ t ≤![]() ,
,
t ![]() ,
,
② PE 不能与 AC 垂直。
若 PE AC ,延长QE 交OA 于 F ,如图 3,
QF ![]() ,
,
EF QF QE QF OQ ![]() (t
(t ![]() - (t
- (t ![]() =(
=(![]()
![]()
又Rt△EPF ∽ Rt△OCA ,
![]() ,
,
t 3.45 .
而0 ≤ t ≤![]() .
.
∴ t 不存在.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①ac>0;②当x>1时,函数y随x的增大而增大;③a+b+c=0;④2a+b=0;⑤当y>0时,﹣1<x<3.其中,正确的说法有( )个
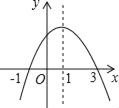
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
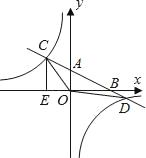
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
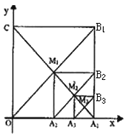
【题目】如图 ,在平面直角坐标系中,边长为 1 的正方形OA1B1C 的对角线 A1C 和OB1 交于点 M1,以 M1A1为对角线作第二个正方形 A2A1B2M1对角线 A1M1和 A2 B2 交于点 M 2 ;以 M 2 A1 为对角线作第三个正方形 A3 A1B3M 2,对角线 A1M 2 和 A3 B3 交于点 M 3 ;…,依此类推,那么 M 1 的坐标为_____;这样作的第 n 个正方形的对角线交点 Mn 的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
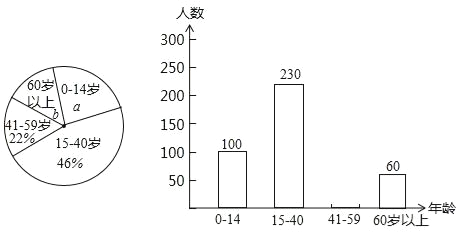
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD的边长为5,∠DAB=60°.将菱形ABCD绕着A逆时针旋转得到菱形AEFG,设∠EAB=α,且0°<α<90°,连接DG、BE、CE、CF.
(1)如图(1),求证:△AGD≌△AEB;
(2)当α=60°时,在图(2)中画出图形并求出线段CF的长;
(3)若∠CEF=90°,在图(3)中画出图形并求出△CEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
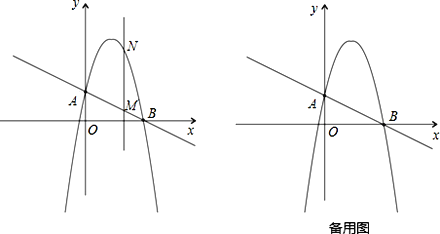
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程![]() 有两个相等的实数根,其中正确的结论是______.(只填序号即可).
有两个相等的实数根,其中正确的结论是______.(只填序号即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com