
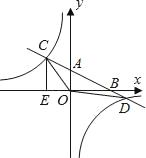
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
【答案】(1)y=﹣![]() x+2,y=﹣
x+2,y=﹣![]() .(2)8.
.(2)8.
【解析】试题分析:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例的函数解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解.
试题解析:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=![]() .
.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(-2,3).
设直线AB的解析式为y=kx+b,则![]() ,
,
解得 .
.
故直线AB的解析式为y=-![]() x+2.
x+2.
设反比例函数的解析式为y=![]() (m≠0),
(m≠0),
将点C的坐标代入,得3=![]() ,
,
∴m=-6.
∴该反比例函数的解析式为y=-![]() .
.
(2)联立反比例函数的解析式和直线AB的解析式可得
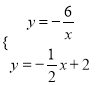 ,
,
可得交点D的坐标为(6,-1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
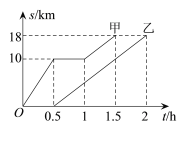
【题目】甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,有下列说法:①甲、乙同学都骑行了18km;②甲、乙同学同时到达B地;③甲停留前、后的骑行速度相同;④乙的骑行速度是![]() ;其中正确的说法是( )
;其中正确的说法是( )
A. ①③B. ①④C. ②④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据
月份n(月)1 | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
(1)稿费不高于800元的不纳税;
(2)稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
(3)稿费为4000元或高于4000元的应缴纳全部稿费的11%的税,
试根据上述纳税的计算方法作答:
①若王老师获得的稿费为2400元,则应纳税________元,若王老师获得的稿费为4000元,则应纳税________元.
②若王老师获稿费后纳税420元,求这笔稿费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后, ![]() 能被x0+3整除,…,
能被x0+3整除,…, ![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2019=( )
A.(31,47)B.(31,48)C.(32,48)D.(32,49)
查看答案和解析>>
科目:初中数学 来源: 题型:
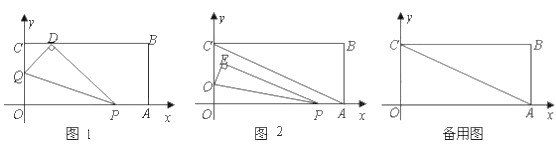
【题目】将一矩形纸片OABC 放在平面直角坐标系中, O(0,0) , A(6,0) , C(0,3) .动点Q 从点O 出发以每秒 1 个单位长的速度沿OC 向终点C 运动,运动![]() 秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
秒时,动点 P 从点A 出发以相等的速度沿 AO 向终点O 运动。当其中一点到达终点时,另一点也停止运动。设点 P 的运动时间为t (秒).
(1)用含t 的代数式表示OP,OQ ;
(2)当t 1时,如图 1,将△OPQ 沿 PQ 翻折,点O 恰好落在CB 边上的点 D 处,求点 D 的坐标;
(3)连结 AC ,将△OPQ 沿 PQ 翻折,得到△EPQ ,如图 2.问: PQ 与 AC 能否平行? PE 与 AC 能否垂直?若能,求出相应的t 值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOD=∠COB=90°,∠COE=25°,EO是∠BOD的角平分线;
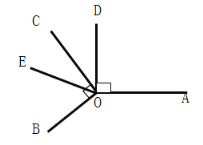
(1)找出图中除直角外的两对相等的角:
(2)求∠COD的度数,按要求填空:
因为∠COB=90°,∠COE=25°,
所以∠BOE=∠ -∠ =90°- °= °.
因为EO是∠BOD的角平分线,
所以∠ =∠BOE= °
所以∠COD=∠ -∠ = °- °= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com