
【题目】如图,∠AOD=∠COB=90°,∠COE=25°,EO是∠BOD的角平分线;
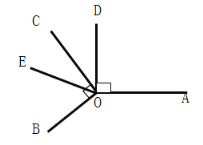
(1)找出图中除直角外的两对相等的角:
(2)求∠COD的度数,按要求填空:
因为∠COB=90°,∠COE=25°,
所以∠BOE=∠ -∠ =90°- °= °.
因为EO是∠BOD的角平分线,
所以∠ =∠BOE= °
所以∠COD=∠ -∠ = °- °= °.
【答案】(1)∠DOE=∠BOE,∠AOC=∠BOD;(2)COB,COE,25,65,DOE,65,DOE,COE,65,25,40.
【解析】
(1)由角平分线可得一对相等的角,再用两个直角分别加上∠COD可得一对相等的角;
(2)先求∠BOE,再根据角平分线得到∠DOE=∠BOE,再用∠DOE减去∠COE即可得到∠COD.
解:(1)∵EO是∠BOD的角平分线,
∴∠DOE=∠BOE
∵∠AOD=∠COB=90°
∴∠AOD+∠COD=∠COB+∠COD
即∠AOC=∠BOD
故填:∠DOE=∠BOE,∠AOC=∠BOD.
(2)因为∠COB=90°,∠COE=25°,
所以∠BOE=∠COB-∠COE=90°-25°=65°,
因为EO是∠BOD的角平分线,
所以∠DOE=∠BOE=65° ,
所以∠COD=∠DOE-∠COE=65°-25°=40°.
故填:COB,COE,25,65,DOE,65,DOE,COE,65,25,40.


科目:初中数学 来源: 题型:
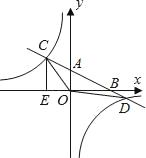
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沾益区兴隆水果店计划用1000元购进甲、乙两种新出产的水果140千克,这两种水果的进价、售价如下表所示:
进价(元/千克) | 售价(元/千克) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)这两种水果各购进多少千克?
(2)该水果店全部销售完这批水果时获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
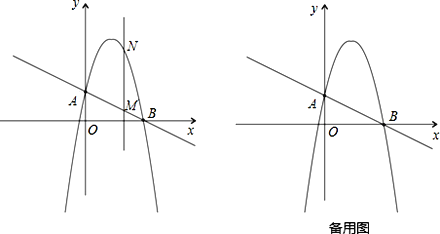
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
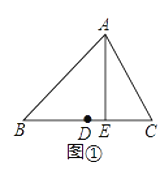
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是________,推断的数学依据是________.
(2)如图②,在△ABC中,∠B=45°,AB=![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.

(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有![]() 的代数式表示相应图形的面积.
的代数式表示相应图形的面积.
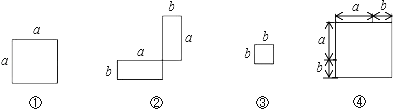
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达: .
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念李时珍诞辰500周年,蕲春县投巨资建设如图所示展览馆,其外框是一个大正方形,中间四个大小相同的正方形(阴影部分)是支展馆的核心筒,标记了字母的五个大小相同的正方形是展厅,剩余的四个大小相同的图形是休息厅,已知核心筒的正方形边长比展厅的正方形边长的一半多1米
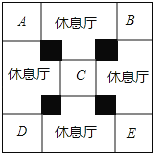
(1)若设展厅的正方形边长为a米,则用含a的代数式表示核心筒的正方形边长为 米.
(2)若设核心筒的正方形边长为b米,求该展馆外框大正方形的周长(用含b的代数式表示).
(3)若展览馆外框大正形边长为26米,求休息厅的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程![]() 有两个相等的实数根,其中正确的结论是______.(只填序号即可).
有两个相等的实数根,其中正确的结论是______.(只填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=![]() MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.
(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com