
【题目】下面的统计图反映了我国邮电业务(含邮政业务与电信业务)总量的情况.
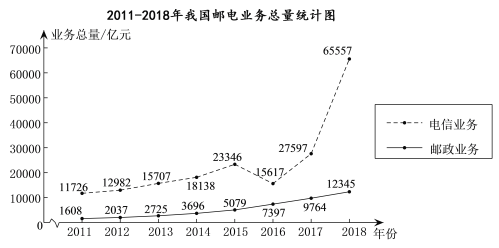
(以上数据来源于国家统计局)
根据统计图提供的信息,下列有关我国邮电业务总量推断不合理的是( )
A. 2018年,电信业务总量比邮政业务总量的5倍还多
B. 2011—2018年,邮政业务总量与电信业务总量都是逐年增长的
C. 与2017年相比,2018年邮政业务总量的增长率超过20%
D. 2011—2018年,电信业务总量年增长的平均值大于邮政业务总量年增长的平均值
【答案】B
【解析】
利用折线统计图结合相应数据,分别分析得出符合题意的答案.
A、∵65557÷12345≈5.31,
∴2018年,电信业务总量比邮政业务总量的5倍还多,说法正确;
B、由折线统计图可得:2011—2018年,邮政业务总量是逐年增长的,而电信业务总量在2015-2016年是下降的,故此选项错误,符合题意;
C、∵(12345-9764)÷9764≈0.264=26.4%,
∴与2017年相比,2018年邮政业务总量的增长率超过20%,推断正确;
D、∵电信业务总量年增长的平均值=![]() =23777.5 亿元,
=23777.5 亿元,
邮政业务总量年增长的平均值=![]() =5581.375亿元,
=5581.375亿元,
∴ 2011—2018年,电信业务总量年增长的平均值大于邮政业务总量年增长的平均值,推断正确.
故选B.


科目:初中数学 来源: 题型:
【题目】某通讯公司推出了移动电话的两种计费方式(详情见下表). 设一个月内使用移动电话主叫的时间为t分钟
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 58元 | 150分钟 | 0.25元/分 | 免费 |
方式二 | 88元 | 350分钟 | 0.19元/分 | 免费 |

(t为正整数),请根据表中提供的信息回答下列问题:
(1)方式一中,当t超过150分钟时,该月费用表示为: 元(用含t的代数式表示);方式二中,当t超过350分钟时,该月费用表示为: 元(用含t的代数式表示).
(2)当t=300时,哪种计费方式的费用较省?请作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
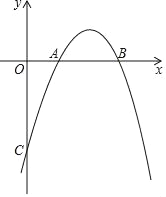
【题目】己知,二次函数y=﹣x2+bx+c的图象与x轴的两个交点A,B的横坐标分别为1和2,与y轴的交点是C.
(1)求这个二次函数的表达式;
(2)若点D是y轴上的一点,是否存在D,使以B,C,D为顶点的三角形与△ABC相似?若存在,求点D的坐标,若不存在,请说明理由;
(3)过点C作CE∥x轴,与二次函数y=﹣x2+bx+c的图象相交于点E,点H是该二次函数图象上的动点,过点H作HF∥y轴,交线段BC于点F,试探究当点H运动到何处时,△CHF与△HFE的面积之和最大,求点H的坐标及最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,有下列说法:①甲、乙同学都骑行了18km;②甲、乙同学同时到达B地;③甲停留前、后的骑行速度相同;④乙的骑行速度是![]() ;其中正确的说法是( )
;其中正确的说法是( )
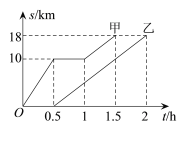
A. ①③B. ①④C. ②④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论
①abc>0;
②4a+b=0;
③9a+c>3b;
④当x>﹣1时,y的值随x值的增大而增大,其中正确的结论有( )
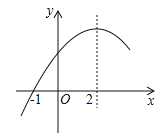
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数运算:
(1)﹣13+28+62﹣77
(2)4﹣4+(﹣3)×(﹣![]() )
)
(3)﹣12006+[1﹣(2﹣22)×3]+(﹣1)2016
(4)(﹣6)×(﹣![]() )×(﹣8)
)×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.
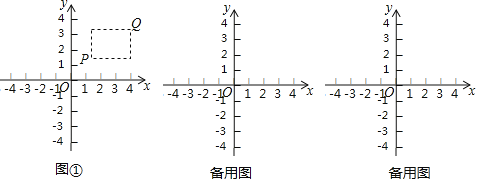
已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后, ![]() 能被x0+3整除,…,
能被x0+3整除,…, ![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2的一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com