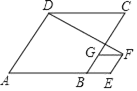
【题目】如图，菱形ABCD和菱形BEFG的边长分别是5和2，∠A＝60°，连结DF，则DF的长为_____．
【答案】
【解析】
延长FG交AD于点M，过点D作DH⊥AB交AB于点H，交GF的延长线于点N，由菱形的性质和勾股定理再结合已知条件可求出NF，DN的长，在直角三角形DNF中，再利用勾股定理即可求出DF的长．
延长FG交AD于点M，过点D作DH⊥AB交AB于点H，交GF的延长线于点N，
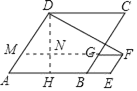
∵四边形ABCD和四边形BEFG都是菱形，
∴GF∥BE，EF∥AM，
∴四边形AMFE是平行四边形，
∴AM＝EF＝2，MF＝AE＝AB+BE＝5+2＝7，
∴DM＝AD﹣AM＝5﹣2＝3，
∵∠A＝60°，
∴∠DAH＝30°，
∴MN＝
DM＝
，
∴DN＝
＝
，NF＝MF﹣MN＝
，
在Rt△DNF中，DF＝
＝，
故答案为：．
阳光课堂课时作业系列答案科目：初中数学 来源： 题型：
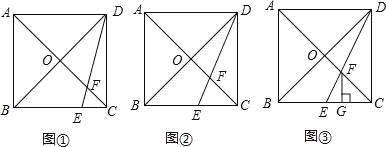
【题目】如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE， 交 AC于点F.
(1)如图①，当
时，求
的值；
(2)如图②当DE平分∠CDB时，求证：AF=
OA；
(3)如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG=
BG.
查看答案和解析>>
科目：初中数学 来源： 题型：
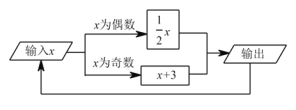
【题目】如图所示的运算程序中，若开始输入的x值为 48，我们发现第一次输出的结果为 24，第二次输出的结果为 12，···，则第 2012 次输出的结果为（ ）
A.3B.6C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
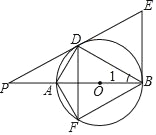
【题目】如图，AB是⊙O的直径，AD、BD是⊙O的弦，且∠PDA=∠1，过点B的切线BE与PD的延长线交于点E．把△PDA沿AD翻折，点P正好落在⊙O的F点上．
（1）证明：PD是⊙O的切线；
（2）求证：DF∥BE；
（3）若PA=2，求四边形BEDF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列关于一元二次方程x2+bx+c＝0的四个命题
①当c＝0，b≠0时，这个方程一定有两个不相等的实数根；
②当c≠0时，若p是方程x2+bx+c＝0的一个根，则
是方程cx2+bx+1＝0的一个根；
③若c＜0，则一定存在两个实数m＜n，使得m2+mb+c＜0＜n2+nb+c；
④若p，q是方程的两个实数根，则p﹣q＝
，
其中是假命题的序号是（ ）
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目：初中数学 来源： 题型：
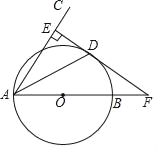
【题目】如图，AB是⊙O的直径，弦AD平分∠BAC，过点D作DE⊥AC于E．
（1）求证：ED是⊙O的切线；
（2）若ED，AB的延长线相交于F，且AE=5，EF=12，求BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：
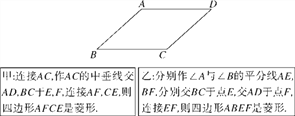
对于甲、乙两人的作法，可判断( )
A. 甲正确，乙错误 B. 甲错误，乙正确
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图①点C在线段AB上，点M、N分别是AC、BC的中点，且满足AC＝a，BC＝b．
（1）若a＝4 cm，b＝6 cm，求线段MN的长；
（2）若点C为线段AB上任意一点，其它条件不变，你能猜想MN的长度吗？直接写出你的猜想结果；
（3）若点C在线段AB的延长线上，其它条件不变，你能猜想MN的长度吗？请在图②中画出图形，写出你的猜想并说明理由．
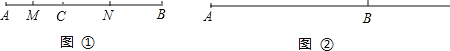
查看答案和解析>>
科目：初中数学 来源： 题型：
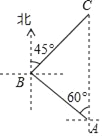
【题目】科技改变生活，手机导航极大方便了人们的出行，如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60°方向行驶12千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B，C两地的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com