
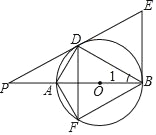
【题目】如图,AB是⊙O的直径,AD、BD是⊙O的弦,且∠PDA=∠1,过点B的切线BE与PD的延长线交于点E.把△PDA沿AD翻折,点P正好落在⊙O的F点上.
(1)证明:PD是⊙O的切线;
(2)求证:DF∥BE;
(3)若PA=2,求四边形BEDF的面积.
科目:初中数学 来源: 题型:
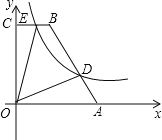
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0), (2,6),点D为AB上一点,且BD=2AD,双曲线y=![]() (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
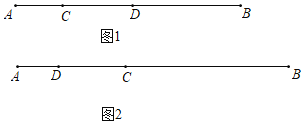
【题目】点C,点D是线段AB上任意两点.
(1)如图1,若点D是线段BC的中点,AD=18,AC=6,求线段BD的长;
(2)如图2,若点C把线段AB分为2:3的两段(AC<BC),点D分线段AB为1:5两段(AD<BD),DC=7,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形 ABCD (如图 1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2 左上角正方形AEMH再作划分,得图3,则图3 中共有9个正方形;
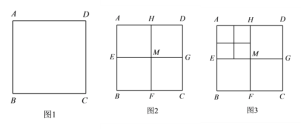
(1)若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有 个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)按这种方法能否将正方形ABCD划分成有2015个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算 ![]() .( 直接写出答案即可)
.( 直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论.
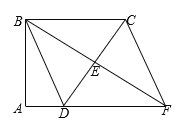
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长均为
的正方形网格中,每个小正方形的边长均为![]() ,每个小正方形的顶点叫做格点.
,每个小正方形的顶点叫做格点.![]() 的顶点都在格点上.按照要求完成下列画图(只在此
的顶点都在格点上.按照要求完成下列画图(只在此![]() 的网格中完成且所画各点都是格点,所画的点可以与已知点重合).
的网格中完成且所画各点都是格点,所画的点可以与已知点重合).

(1)将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ;
;
(2)画出所有点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)画出一个与![]() 相似(但不全等)的三角形
相似(但不全等)的三角形![]() ,且
,且![]() 与
与![]() 有公共点
有公共点![]() (画出一个三角形即可).
(画出一个三角形即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com