
【题目】如图,一次函数y=x+4的图像与反比例函数![]() (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且![]() ,求点P的坐标.
,求点P的坐标.

【答案】(1)![]() ;(2)点P(-6,0)或(-2,0).
;(2)点P(-6,0)或(-2,0).
【解析】
(1)把A点坐标代入直线解析式求出a的值,再把A(-1,3)代入反比例函数关系式中,求出k的值即可;
(2)分别求出B、C的坐标,设点P的坐标为(x,0),根据![]() 列出方程求解即可.
列出方程求解即可.
(1)把点A(-1,a)代入y=x+4,得a=3, ∴A(-1,3),∴k=-3,
∴反比例函数的表达式为y=-![]() ;
;
(2)把B(b,1)代入反比例函数y=-![]() ,
,
解得:b=-3,∴B(-3,1),
当y=x+4=0时,得x=-4,
∴点C(-4,0),
设点P的坐标为(x,0),
∵S△AOB=S△AOC-S△BOC=![]() ×4×3-
×4×3-![]() ×4×1=6-2=4,S△ACP=
×4×1=6-2=4,S△ACP=![]() S△AOB,
S△AOB,
∴![]() ×3×│x-(-4)│=
×3×│x-(-4)│=![]() ×4=3,
×4=3,
解得x1=-6,x2=-2,
∴点P(-6,0)或(-2,0).


科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是BC边上一点,F是BA延长线上一点,AF=CE,连接BD,EF,FG平分∠BFE交BD于点G.
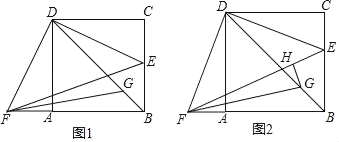
(1)求证:△ADF≌△CDE;
(2)求证:DF=DG;
(3)如图2,若GH⊥EF于点H,且EH=![]() FH,设正方形ABCD的边长为x,GH=y,求y与x之间的关系式.
FH,设正方形ABCD的边长为x,GH=y,求y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) | 水价(元/吨) |
第一级 20吨以下(含20吨) | 1.6 |
第二级 20吨﹣30吨(含30吨) | 2.4 |
第三级 30吨以上 | 3.2 |
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论.
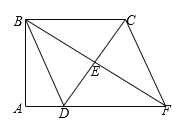
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分师生要去外地参加夏令营活动,车站提出两种车票价格优惠方案供学校选择:第一种方案是教师按原价付款,学生按原价的75%付款;第二种方案是师生都按原价的80%付款.已知该校有5名教师和x名学生参加此次夏令营活动,车票原价为100元/张.
(1)分别写出两种方案的购票款(列代数式并化简)
(2)如果两种方案的付款相同,那么参加夏令营的学生有多少人?
(3)当参加夏令营的学生人数为![]() 名时,试说明选择哪一种方案购票省钱?
名时,试说明选择哪一种方案购票省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何计算
(1)如图1,∠AOC,∠BOD都是直角,且∠AOB与∠AOD的度数比是2:11,求∠BOC的度数.
(2)如图2,点C分线段AB为3:4,AC<BC,点D分线段为AB上一点且11BD=3AD,若CD=10cm,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
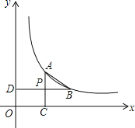
【题目】(1)如图,已知点A、B在双曲线![]() (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,点B的横坐标为b.A与B的坐标分别为_____、______(用b与k表示),由此可以猜想AP与CP的数量关系是______.
(x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,点B的横坐标为b.A与B的坐标分别为_____、______(用b与k表示),由此可以猜想AP与CP的数量关系是______.
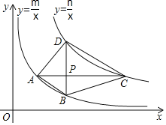
(2)四边形ABCD的四个顶点分别在反比例函数y![]() 与y
与y![]() 的图象上,对角线BD∥y轴,且BD⊥AC于点P,P是BD的中点,点B的横坐标为4.
的图象上,对角线BD∥y轴,且BD⊥AC于点P,P是BD的中点,点B的横坐标为4.
①当![]() 时,判断四边形ABCD的形状并说明理由.
时,判断四边形ABCD的形状并说明理由.
②四边形ABCD能否成为正方形?若能,直接写出此时m,n之间的数量关系;若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
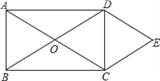
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE∥AC,CE∥BD,DE、CE相交于点E.求证:
(1)四边形OCED是菱形.
(2)连接OE,若AD=4,CD=3,求菱形OCED的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com