
【题目】如图1,在正方形ABCD中,E是BC边上一点,F是BA延长线上一点,AF=CE,连接BD,EF,FG平分∠BFE交BD于点G.
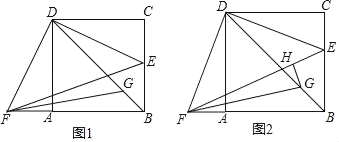
(1)求证:△ADF≌△CDE;
(2)求证:DF=DG;
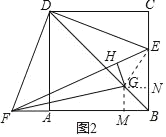
(3)如图2,若GH⊥EF于点H,且EH=![]() FH,设正方形ABCD的边长为x,GH=y,求y与x之间的关系式.
FH,设正方形ABCD的边长为x,GH=y,求y与x之间的关系式.
【答案】(1)详见解析;(2)详见解析;(3)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据SAS即可证明;
(2)欲证明DF=DG,只要证明∠DFG=∠DGF;
(3)如图2中,作GM⊥AB于M,GN⊥BC于N.连接EG.首先说明G是△BEF的内心,由题意Rt△FGH≌Rt△FGM,Rt△EGH≌Rt△EGN,四边形GMBN是正方形,推出FH=FM,EH=EN,GN=GM=BM=BN=y,由EH:FH=1:3,设EH=a,则FH=3a,FB=3a+y,BE=a+y,EC=AF,推出FB+BE=2x,可得3a+y+a+y=2x,即y=x-2a,推出CN=2a,推出CE=a,想办法用a表示x、y即可解决问题;
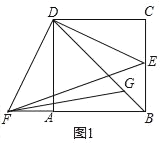
(1)证明:如图1中,∵四边形ABCD是正方形,
∴∠C=∠BAD=∠DAF=90°,CD=DA,
在△ADF和△CDE中,
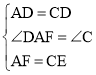
∴△ADF≌△CDE.
(2)证明:如图1中,∵四边形ABCD是正方形,
∴∠FBG=45°,
∵△ADF≌△CDE,
∴DF=DE,∠ADF=∠CDE,
∴∠EDF=∠ADC=90°,
∠DFE=45°,
∵∠DFG=45°+∠EFG,∠DGF=45°+∠GFB,
∵∠EFG=∠BFG,
∴∠DFG=∠DGF,
∴DF=DG.
(3)结论:![]()
理由:如图2中,作GM⊥AB于M,GN⊥BC于N.连接EG.
∵GF平分∠BAE,DB平分∠EBF,
∴G是△BEF的内心,∵GH⊥EF,
∴GH=GN=GM=y,
∵FG=FG,EG=EG,
∴Rt△FGH≌Rt△FGM,Rt△EGH≌Rt△EGN,四边形GMBN是正方形,
∴FH=FM,EH=EN,GN=GM=BM=BN=y,
∵EH:FH=1:3,设EH=a,则FH=3a,
∵FB=3a+y,BE=a+y,
∵EC=AF,
∴FB+BE=2x,
∴3a+y+a+y=2x,
∴y=x﹣2a,
∴CN=2a,
∵EN=EH=a,
∴CE=a,
在Rt△DEF中,DE=2![]() a,
a,
在Rt△DCE中,![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2.过点A作对角线BD的平行线与边CD的延长线相交于点E.P为边BD上的一个动点(不与端点B,D重合),连接PA,PE,AC.
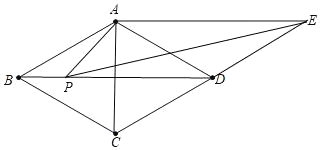
(1)求证:四边形ABDE是平行四边形;
(2)求四边形ABDE的周长和面积;
(3)记△ABP的周长和面积分别为C1和S1,△PDE的周长和面积分别为C2和S2,在点P的运动过程中,试探究下列两个式子的值或范围:①C1+C2,②S1+S2,如果是定值的,请直接写出这个定值;如果不是定值的,请直接写出它的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)8+(―![]() )―(―0.25)
)―(―0.25)
(2)-63÷7+45÷(-9)
(3)(-3)×(-9)-8×(-5)
(4)(-0.1)3-![]()
(5)-23-3×(-2)3-(-1)4
(6)(-![]()
(7)[11×2-|3÷3|-(-3)2-33]÷![]()
(8)2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,从图中可以看出,终点表示的数是﹣2,已知A,B是数轴上的点.请参照图并思考,完成下列填空:
(1)如果点A表示数3,将点A向右移动7个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(2)如果点B表示数2,将点B向左移动9个单位长度,再向右移动5个单位长度,那么终点A表示的数是 ,A,B两点间的距离是 .

(3)如果点A表示的数是﹣4,将点A向右移动168个单位长度;再向左移动2个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是 ,A,B两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知式子 ![]() 是关于x的二次多项式,且二次项系数为b,数轴上A、B两点所对应的数分别是a和b.
是关于x的二次多项式,且二次项系数为b,数轴上A、B两点所对应的数分别是a和b.

(1)则a=____,b=____.A、B两点之间的距离:____;
(2)有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2019次时,求点P所对应的有理数.
(3)在(2)的条件下,点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距零离是点P到点A的距离的3倍?若可能请求出此时点P的位置,若不可能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寻找公式,求代数式的值:从2开始,连续的的偶数相加,它们的和的情况如下表:

(1)根据上面的等式,你能发现当n个连续的的偶数相加时,它们的和S=2+4+6+8+……+2n= .
(2)并按照此规律计算:①2+4+6+……300的值;②162+164+166+……+400的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知从甲地到乙地,某船顺水航行需2小时,逆水航行需3小时,
(1)设轮船在静水中前进的速度是![]() 千米/时,水流的速度是y千米/时,则轮船共航行多少千米?
千米/时,水流的速度是y千米/时,则轮船共航行多少千米?
(2)如果轮船在静水中前进的速度是60千米/时,则水流的速度是多少千米/时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图像与反比例函数![]() (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com