
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是 米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).
![]()
【答案】(1)450;(2)机器人前3分钟的速度为80米/分;(3)两机器人前6分钟内出发![]() 分或
分或![]() 分时相距28米;(4)见解析.
分时相距28米;(4)见解析.
【解析】
(1)根据题目中的数据可以求得B、C两点之间的距离;
(2)根据题意,可以得到甲机器人前3分钟的速度;
(3)根据题意可知前4分钟甲机器人的速度,在4≤t≤6分钟时,甲的速度,从而可以求得两机器人前6分钟内出发多长时间相距28米;
(4)根据题意可以得到当t>6时,甲、乙两机器人之间的距离S.
解:(1)由题意可得,
B、C两点之间的距离是:50×9=450(米),
故答案为:450;
(2)设甲机器人前3分钟的速度为a米/分,
3a=90+3×50,
解得,a=80,
答:机器人前3分钟的速度为80米/分;
(3)∵前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,
∴前4分钟甲机器人的速度为80米/分,在4≤t≤6分钟时,甲的速度为50米/分,
设甲乙相遇前相距28米时出发的时间为b分钟,
80b+28=90+50b,
解得,b=![]() ,
,
设甲乙相遇后相距28米时出发的时间为c分钟,
80c﹣28=90+50c,
解得,c=![]() ,
,
答:两机器人前6分钟内出发![]() 分或
分或![]() 分时相距28米;
分时相距28米;
(4)∵6分钟后甲机器人的速度又恢复为原来出发时的速度,
∴6分钟后甲机器人的速度是80米/分,
当t=6时,甲乙两机器人的距离为:[80×4+50×(6﹣2)]﹣(90+50×6)=60(米),
当甲到达终点C时,t={(90+450)﹣[80×4+50×(6﹣2)]}÷80+6=7.5(分),
当乙到达终点C时,t=450÷50=9(分),
∴当6<t≤7.5时,S=60+(80﹣50)×(t﹣6)=30t﹣120,
当7.5<t≤9时,S=450﹣50×7.5﹣50(t﹣7.5)=﹣50t+450,
由上可得,当t>6时,甲、乙两机器人之间的距离S=![]() .
.


科目:初中数学 来源: 题型:
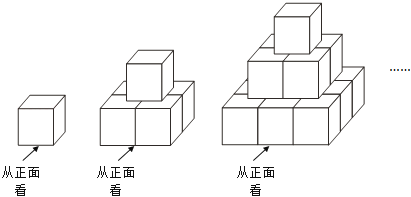
【题目】现用棱长为1cm的若干小立方体,按如图所示的规律在地上搭建若个几何体.图中每个几何体自上而下分别叫第一层,第二层…第n层(n为正整数),其中第一层摆放一个小立方体,第二层摆放4个小立方体,第三层摆放9个小立方体…,依次按此规律继续摆放.
(1)求搭建第4个几何体需要的小立方体个数;
(2)为了美观,若将每个几何体的所有露出部分(不包含底面)都喷涂油漆,已知喷涂1cm2需要油漆0.2g.
①求喷涂第4个几何体需要油漆多少g?
②求喷涂第n个几何体需要油漆多少g?(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,线段AB=8cm,点C为线段AB上的一个动点(点C不与点A、B重合),D、E分别是线段AC和线段BC的中点.
(1)求DE的长;
(2)知识迁移:如图②,已知∠AOB=![]() ,射线OC在∠AOB的内部,若OD、OE分别平分∠AOC和∠BOC,求∠DOE的度数(用含
,射线OC在∠AOB的内部,若OD、OE分别平分∠AOC和∠BOC,求∠DOE的度数(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
(1)填出下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 |
(2)如果剪了100次,共剪出 个小正方形?
(3)如果剪![]() 次,共剪出 个小正方形?
次,共剪出 个小正方形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )
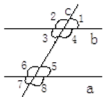
A. ①② B. ①③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
求证:(1)AB是∠CAF的角平分线;
(2)∠FAD = ∠E.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线 ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.点P为线段BC上一点,过点P作直线ι⊥x轴于点F,交抛物线 ![]() 于点E.
于点E.
(1)求A、B、C三点的坐标;
(2)当点P在线段BC上运动时,求线段PE长的最大值;
(3)当PE取最大值时,把抛物线 ![]() 向右平移得到抛物线
向右平移得到抛物线 ![]() ,抛物线
,抛物线 ![]() 与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线
与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线 ![]() 应向右平移几个单位长度可得到抛物线
应向右平移几个单位长度可得到抛物线 ![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com