
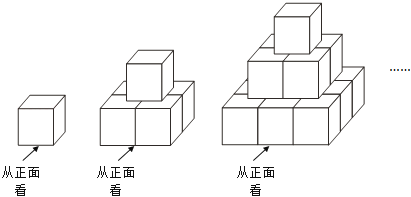
【题目】现用棱长为1cm的若干小立方体,按如图所示的规律在地上搭建若个几何体.图中每个几何体自上而下分别叫第一层,第二层…第n层(n为正整数),其中第一层摆放一个小立方体,第二层摆放4个小立方体,第三层摆放9个小立方体…,依次按此规律继续摆放.
(1)求搭建第4个几何体需要的小立方体个数;
(2)为了美观,若将每个几何体的所有露出部分(不包含底面)都喷涂油漆,已知喷涂1cm2需要油漆0.2g.
①求喷涂第4个几何体需要油漆多少g?
②求喷涂第n个几何体需要油漆多少g?(用含n的代数式表示)
【答案】(1)30;(2)①11.2(g).②(0.6n2+0.4n)g.
【解析】
试题分析:(1)观察得到每层向上的面都为正方形,即每层的个数都为平方数,则搭建第4个几何体的小立方体的个数=1+4+9+16;第n个几何体第n层的个数为n2,所以总数为1+22+32+42+…+n2;
(2)①喷漆第四个几何露在外面的表面积为:4×(1+2+3+4)+42=56(cm2),再用表面积×0.2,即可解答.
②第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2,化简后乘以0.2即可.
解:(1)搭建第4个几何体的小立方体的个数=1+4+9+16=30;
(2)①喷漆第四个几何露在外面的表面积为:4×(1+2+3+4)+42=56(cm2),
56×0.2=11.2(g).
②第n个几何体的所有露出部分(不含底面)的面积=4×(1+2+3+…+n)+n2=4×![]() +n2=3n2+2n,
+n2=3n2+2n,
所以所需要的油漆量=(3n2+2n)×0.2=(0.6n2+0.4n)g.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在公式(a+1)2=a2+2a+1中,当a分别取1,2,3,4,…,n时,可得以下等式:
(1+1)2=12+2×1+1;
(2+1)2=22+2×2+1;
(3+1)2=32+2×3+1;
(4+1)2=42+2×4+1;
……
(n+1)2=n2+2n+1.
将这几个等式的左右两边分别相加,可以推导出求和公式:1+2+3+4+…+n=![]() .
.
请写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 的图像与反比例函数
的图像与反比例函数 ![]() (
( ![]() 为常数,且
为常数,且 ![]() )的图像都经过点
)的图像都经过点 ![]()

(1)求点 ![]() 的坐标及反比例函数的表达式;
的坐标及反比例函数的表达式;
(2)结合图像直接比较:当 ![]() 时,
时, ![]() 和
和 ![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形AOB和三角形COD中,∠AOB=∠COD,
(1)已知∠AOB=90°,把两个三角形拼成如图①所示的图案,当∠BOD=30°时,求∠AOC的度数.
(2)已知∠AOB=90°,把两个三角形拼成如图②所示的图案,当∠AOC=2∠BOD时,求∠BOD的度数.
(3)当∠AOB=α时,把两个三角形拼成如图③所示的图案.用含有α的代数式表示∠AOC+∠BOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似。如图,如果扇形AOB与扇形 ![]() 是相似扇形,且半径
是相似扇形,且半径 ![]() (
( ![]() 为不等于0的常数)。那么下面四个结论:①∠AOB=∠
为不等于0的常数)。那么下面四个结论:①∠AOB=∠ ![]() ;②△AOB∽△
;②△AOB∽△ ![]() ;③
;③ ![]() ;④扇形AOB与扇形
;④扇形AOB与扇形 ![]() 的面积之比为
的面积之比为 ![]() 。成立的个数为:( )
。成立的个数为:( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
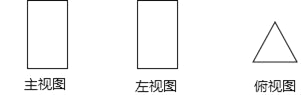
【题目】已知如图为一几何体的三视图:主视图和左视图都是长方形,俯视图是等边三角形
(1)写出这个几何体的名称;
(2)若主视图的高为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、M两点,若点M的坐标是(-4,-2),则点N的坐标为( )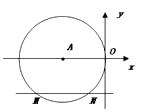
A.(-1,-2)
B.(1,2)
C.(-1.5,-2)
D.(1.5,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是 米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com