
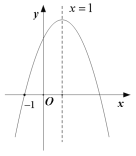
【题目】抛物线![]() 的图象如图所示,抛物线过点
的图象如图所示,抛物线过点![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为一切实数);⑤
为一切实数);⑤![]() ;正确的个数有( ).
;正确的个数有( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】
由抛物线开口方向,对称轴的位置以及与![]() 轴的交点位置,确定
轴的交点位置,确定![]() 的正负,即可①;抛物线y=ax2+bx+c的对称轴为x=
的正负,即可①;抛物线y=ax2+bx+c的对称轴为x=![]() ,即可判断②;抛物线与x轴的一个交点 (
,即可判断②;抛物线与x轴的一个交点 (![]() ,0),得到另一个交点,把b=2a代入即可判断③,根据抛物线的最大值判断④;由抛物线与x轴有两个交点得到b2-4ac>0,即可判断⑤.
,0),得到另一个交点,把b=2a代入即可判断③,根据抛物线的最大值判断④;由抛物线与x轴有两个交点得到b2-4ac>0,即可判断⑤.
①∵抛物线开口向下,
∴a<0,
∵对称轴是:![]()
∴a、b异号,
∴b>0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,
∴选项①不正确;
②抛物线对称轴是:![]()
b=2a,
2a+b=0,
选项②不正确;
③抛物线与x轴的一个交点 (![]() ,0),则另一个交点为(
,0),则另一个交点为(![]() ,0),
,0),
![]()
把b=2a代入得:![]()
∴选项③不正确;
④抛物线在![]() 时取得最大值,
时取得最大值,
![]()
即![]()
故选项④不正确;
⑤ ∵抛物线与x轴有两个交点,
∴b2-4ac>0
即![]()
∴选项⑤正确;
正确的有1个,
故选:A


科目:初中数学 来源: 题型:
【题目】将抛物线C:y=x2+3x-10平移到C′.若两条抛物线C,C′关于直线x=1对称,则下列平移方法中正确的是( )
A. 将抛物线C向右平移![]() 个单位 B. 将抛物线C向右平移3个单位
个单位 B. 将抛物线C向右平移3个单位
C. 将抛物线C向右平移5个单位 D. 将抛物线C向右平移6个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
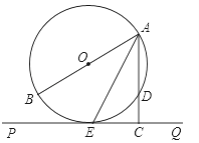
【题目】如图,AB为⊙O的直径,PQ切⊙O于E,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=2,EC=![]() ,∠BAC=60°,求⊙O的半径.
,∠BAC=60°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在目前万物互联的时代,人工智能正掀起一场影响深刻的技术革命.谷歌、苹果、BAT、华为……巨头们纷纷布局人工智能。有人猜测,互联网过后,我们可能会迎来机器人。教育从幼儿抓起,近年来我国国内幼儿教育机器人发展趋势迅猛,市场上出现了满足各类要求的幼教机器人产品.“双十一”当天,某品牌幼教机器人专卖店抓住机遇,对最畅销的![]() 款幼教机器人进行促销,一台
款幼教机器人进行促销,一台![]() 款幼教机器人的成本价为850元,标价为1300元.
款幼教机器人的成本价为850元,标价为1300元.
(1)一台![]() 款幼教机器人的价格最多降价多少元,才能使利润率不低于30%;
款幼教机器人的价格最多降价多少元,才能使利润率不低于30%;
(2)该专卖店以前每周共售出![]() 款幼教机器人100个,“双十一”狂购夜中每台
款幼教机器人100个,“双十一”狂购夜中每台![]() 款幼教机器人在标价的基础上降价
款幼教机器人在标价的基础上降价![]() 元,结果这天晚上卖出的
元,结果这天晚上卖出的![]() 款幼教机器人的数量比原来一周卖出的
款幼教机器人的数量比原来一周卖出的![]() 款幼教机器人的数量增加了
款幼教机器人的数量增加了![]() ,同时这天晚上的利润比原来一周的利润增加了
,同时这天晚上的利润比原来一周的利润增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
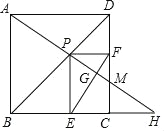
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论_____.(填写序号)
.其中正确结论_____.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
小凯遇到这样一个问题:如图①,在四边形ABCD中,对角线AC,BD相交于点O,AC=4,BD=6,∠AOB=30°,求四边形ABCD的面积.小凯发现,分别过点A,C作直线BD的垂线,垂足分别为E,F,设AO为m,通过计算△ABD与△BCD的面积和可以使问题得到解决(如图②).请回答:
(1)△ABD的面积为________(用含m的式子表示);
(2)求四边形ABCD的面积.
参考小凯思考问题的方法,解决问题:
如图③,在四边形ABCD中,对角线AC,BD相交于点O,AC=a,BD=b,∠AOB=α(0°<α<90°),则四边形ABCD的面积为________(用含a,b,α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tanθ=![]() ;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=
;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=![]() ,求值:
,求值:
(1)tanθ+![]() ; (2)|cosθ-sinθ|.
; (2)|cosθ-sinθ|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com