
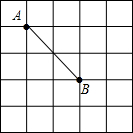
 如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样的点C共8个.
如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样的点C共8个. 科目:初中数学 来源: 题型:解答题
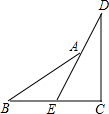 如图,阅读下面的题目及分析过程,并按要求进行证明.
如图,阅读下面的题目及分析过程,并按要求进行证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
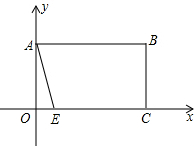 如图,在平面直角坐标系中,四边形OABC是矩形,其中点B的坐标为(5,3),点E在x轴上,将矩形OABC沿AE折叠,点B恰好落在x轴上,求折痕的解析式.
如图,在平面直角坐标系中,四边形OABC是矩形,其中点B的坐标为(5,3),点E在x轴上,将矩形OABC沿AE折叠,点B恰好落在x轴上,求折痕的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
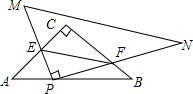 如图,在等腰直角三角形ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,Rt△PMN的直角顶点P在线段AB上,PM、PN分别交于AC、BC于点E、F,PA:PB=1:2,∠BPF=15°,则EF的长为$\frac{2\sqrt{30}}{3}$.
如图,在等腰直角三角形ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,Rt△PMN的直角顶点P在线段AB上,PM、PN分别交于AC、BC于点E、F,PA:PB=1:2,∠BPF=15°,则EF的长为$\frac{2\sqrt{30}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的一元二次方程mx2+(3m+1)x+3=0.
已知关于x的一元二次方程mx2+(3m+1)x+3=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
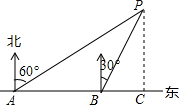 如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.
如图,小聪同学在东西走向的文一路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东90米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到文一路的距离PC为45$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com