Question

如图，是的直径，是的中点，的切线交的延长线于点，是的中点，的延长线交切线于点，交于点，连接.

（1）求证：；

（2）若，求的长.

 

 

Answer 1

(1)证明见解析

(2)

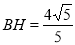
【解析】

试题分析：(1)连接OC，若要证明C为AD的中点，只需证OC//BD，已知C是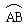的中点，可知OC⊥AB，又BD是切线，可知BD⊥AB，问题得证

(2)由（1）及E为OB中点可知△COE≌△FBE，从而可知BF=CO=BO=2，由勾股定理可得AF的长，由面积法即可求出BH的长

试题解析：（1）连接OC

∵C是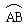的中点，AB是⊙O的直径

∴OC⊥AB

∵BD是⊙O的切线

∴BD⊥AB

∴OC//BD

∵AO=BO

∴AC=CD

（2）∵E是OB的中点

∴OE=BE

在△COE和△FBE中

∴△COE≌△FBE（ASA)

∴BF=CO

∵OB=2

∴BF=2

∴AF=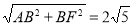

∵AB是直径

∴BH⊥AF

考点：1、平行线分线段成比例定理；2、切线的性质；3勾股定理；4、全等三角形