
如图①,直线l:y=mx+n(m>0,n<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m,n的代数式表示);
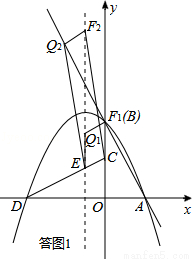
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
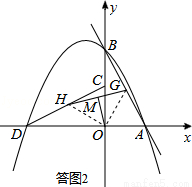
(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM= ,直接写出l,P表示的函数解析式.
,直接写出l,P表示的函数解析式.

(1)y=﹣x2﹣x+2;y=﹣4x+4.
(2)P的对称轴为x=﹣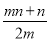 .
.
(3)点Q坐标为Q1(﹣1, )、Q2(﹣1,
)、Q2(﹣1,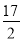 ).
).
(4)l表示的函数解析式为:y=﹣2x+4;P:y=﹣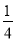 x2﹣x+8.
x2﹣x+8.
【解析】
试题分析:(1)若l:y=﹣2x+2,求出点A、B、D的坐标,利用待定系数法求出P表示的函数解析式;若P:y=﹣x2﹣3x+4,求出点D、A、B的坐标,再利用待定系数法求出l表示的函数解析式;
(2)根据已知求得抛物线与x轴交点的坐标,从而求得对称轴;
(3)以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,则有FQ∥CE,且FQ=CE.以此为基础,列方程求出点Q的坐标.注意:点Q的坐标有两个,如答图1所示,不要漏解;
(4)如答图2所示,作辅助线,构造等腰直角三角形OGH,求出OG的长度,进而由AB=2OG求出AB的长度,再利用勾股定理求出y=mx﹣4m中m的值,最后分别求出l,P表示的函数解析式.
试题解析:(1)若l:y=﹣2x+2,则A(1,0),B(0,2).
∵将△AOB绕点O逆时针旋转90°,得到△COD,
∴D(﹣2,0).
设P表示的函数解析式为:y=ax2+bx+c,将点A、B、D坐标代入得:
 ,解得
,解得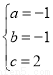 ,
,
∴P表示的函数解析式为:y=﹣x2﹣x+2;
若P:y=﹣x2﹣3x+4=﹣(x+4)(x﹣1),则D(﹣4,0),A(1,0).
∴B(0,4).
设l表示的函数解析式为:y=kx+b,将点A、B坐标代入得:
 ,解得
,解得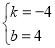 ,
,
∴l表示的函数解析式为:y=﹣4x+4.
(2)直线l:y=mx+n(m>0,n<0),
令y=0,即mx+n=0,得x=﹣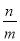 ;令x=0,得y=n.
;令x=0,得y=n.
∴A(﹣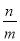 ,0)、B(0,n),
,0)、B(0,n),
∴D(﹣n,0).
设抛物线对称轴与x轴的交点为N(x,0),
∵DN=AN,∴﹣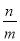 ﹣x=x﹣(﹣n),
﹣x=x﹣(﹣n),
∴2x=﹣n﹣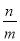 ,
,
∴P的对称轴为x=﹣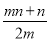 .
.
(3)若l:y=﹣2x+4,则A(2,0)、B(0,4),
∴C(0,2)、D(﹣4,0).
可求得直线CD的解析式为:y= x+2.
x+2.
由(2)可知,P的对称轴为x=﹣1.
∵以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形,
∴FQ∥CE,且FQ=CE.
设直线FQ的解析式为:y= x+b.
x+b.
∵点E、点C的横坐标相差1,∴点F、点Q的横坐标也是相差1.
则|xF﹣(﹣1)|=|xF+1|=1,
解得xF=0或xF=﹣2.
∵点F在直线l:y=﹣2x+4上,∴点F坐标为(0,4)或(﹣2,8).
若F(0,4),则直线FQ的解析式为:y= x+4,当x=﹣1时,y=
x+4,当x=﹣1时,y= ,∴Q1(﹣1,
,∴Q1(﹣1, );
);
若F(﹣2,8),则直线FQ的解析式为:y= x+9,当x=﹣1时,y=
x+9,当x=﹣1时,y=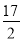 ,∴Q2(﹣1,
,∴Q2(﹣1,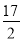 ).
).
∴满足条件的点Q有2个,如答图1所示,点Q坐标为Q1(﹣1, )、Q2(﹣1,
)、Q2(﹣1,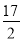 ).
).
(4)如答图2所示,连接OG、OH.
∵点G、H为斜边中点,∴OG= AB,OH=
AB,OH= CD.
CD.
由旋转性质可知,AB=CD,OG⊥OH,
∴△OGH为等腰直角三角形.
∵点G为GH中点,∴△OMG为等腰直角三角形,
∴OG=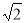 OM=
OM=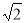 •
•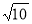 =2
=2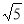 ,
,
∴AB=2OG=4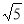 .
.
∵l:y=mx﹣4m,∴A(4,0),B(0,﹣4m).
在Rt△AOB中,由勾股定理得:OA2+OB2=AB2,即:42+(﹣4m)2=(4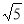 )2,
)2,
解得:m=﹣2或m=2,
∵点B在y轴正半轴,∴m=2舍去,∴m=﹣2.
∴l表示的函数解析式为:y=﹣2x+4;
∴B(0,8),D(﹣8,0).又A(4,0),利用待定系数法求得P:y=﹣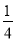 x2﹣x+8.
x2﹣x+8.
考点:1、二次函数的图象与性质;2、待定系数法;3、旋转变换;4、平行四边形


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
在函数y= 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x≥﹣2且x≠1 B.x≤2且x≠1 C.x≠1 D.x≤﹣2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:解答题
某校九年级四个数学活动小组参加测量操场旗杆高度的综合时间活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角级记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和计算数据如下表所示:
组别数据 | CD的长(m) | BC的长(m) | 仰角α | AB的长(m) |
第一组 | 1.59 | 1.32 | 32° | 9.8 |
第二组 | 1.54 | 13.4 | 31° | 9.6 |
第三组 | 1.57 | 14.1 | 30° | 9.7 |
第四组 | 1.56 | 15.2 | 28° |
|
(1)利用第四组学生测量的数据,求旗杆AB的高度(精确到0.1m);
(2)四组学生测量旗杆高度的平均值为 m(精确到0.1m).

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:填空题
如图,将半径为3的圆形纸片,按下列顺序折叠.若 和
和 都经过圆心O,则阴影部分的面积是 (结果保留π)
都经过圆心O,则阴影部分的面积是 (结果保留π)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
如图, 是
是 的直径,
的直径, 是
是 的中点,
的中点, 的切线
的切线 交
交 的延长线于点
的延长线于点 ,
, 是
是 的中点,
的中点, 的延长线交切线
的延长线交切线 于点
于点 ,
, 交
交 于点
于点 ,连接
,连接 .
.
(1)求证: ;
;
(2)若 ,求
,求 的长.
的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:选择题
某商品先按批发价a元提高10%零售,后又按零售价降低10%出售,则最后的单价是( )
A.a元 B.0.99a元 C.1.21a元 D.0.81a元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com