
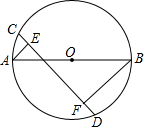
 如图,在⊙O中,AB是直径,CD是弦,过点A、B两点分别作CD的垂线,垂足分别是点E、F,AE=1,BF=3,CD=6,求EF的长.
如图,在⊙O中,AB是直径,CD是弦,过点A、B两点分别作CD的垂线,垂足分别是点E、F,AE=1,BF=3,CD=6,求EF的长. 分析 过点O作OG⊥CD于点G,连接OD,延长BF交⊙O于点H,连接AH,先根据AE⊥CD,BF⊥CD得出△AEF∽△BFI,故可得出$\frac{AE}{BF}$=$\frac{AI}{BI}$=$\frac{1}{3}$,再由点O是AB的中点得出AI=OI,由AAS定理得出△AIE≌△OIG,故AE=OG=1,判断出AEFH是矩形,在Rt△OGD中根据勾股定理求出OD的长,故可得出AB的长,再由勾股定理求出AH的长,由此可得出结论.
解答 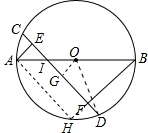 解:过点O作OG⊥CD于点G,连接OD,延长BF交⊙O于点H,连接AH,
解:过点O作OG⊥CD于点G,连接OD,延长BF交⊙O于点H,连接AH,
∵AE⊥CD,BF⊥CD,AE=1,BF=3,
∴△AEF∽△BFI,
∴$\frac{AE}{BF}$=$\frac{AI}{BI}$=$\frac{1}{3}$.
∵点O是AB的中点,
∴OA=OB,
∴AI=OI.
在△AIE与△OIG中,
$\left\{\begin{array}{l}∠AEI=∠OGI\\∠AIE=∠OIE\\ AI=OI\end{array}\right.$,
∴△AIE≌△OIG(AAS),
∴AE=OG=1.
∵CD=3,OG⊥CD,
∴GD=3,
∴OD=$\sqrt{{OG}^{2}+{GD}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$.
∵AB是⊙O的直径,
∴∠AHB=90°.
∵∠AEF=∠EFH=90°,
∴四边形AEFH是矩形,
∴AE=FH=1,AH=EF,
∵BH=3+1=4,
∴AH=$\sqrt{{AB}^{2}-{BH}^{2}}$=$\sqrt{{(2\sqrt{10})}^{2}-{4}^{2}}$=$\sqrt{40-16}$=2$\sqrt{6}$,
∴EF=2$\sqrt{6}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-6x)(2x-3y)=-12x2-18xy | |
| B. | 5x(3x2-2x+3)=15x2-10x2+3 | |
| C. | 4ab[2a2b-3b(ab-ab2)]=8a3b2-12ab2(4a2b2-4a2b3) | |
| D. | a(a+b)-b(a+b)=a2-b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com