
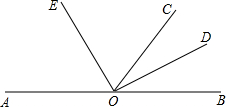
 A、O、B在同一条直线上,OD、OE分别平分∠AOC、∠BOC.
A、O、B在同一条直线上,OD、OE分别平分∠AOC、∠BOC.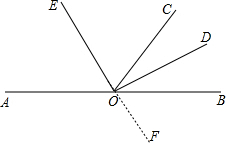


科目:初中数学 来源: 题型:
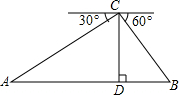 如图,四川汶川地区灾后修建铁路时,要建一条从A到B的隧道,测得山顶C到隧道的垂直高度CD为150m,从山顶C测得A点的俯角为30°,测得B点的俯角为60°,求隧道AB的长.
如图,四川汶川地区灾后修建铁路时,要建一条从A到B的隧道,测得山顶C到隧道的垂直高度CD为150m,从山顶C测得A点的俯角为30°,测得B点的俯角为60°,求隧道AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:
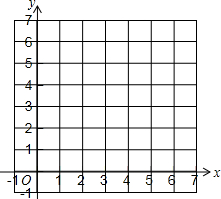 【探索研究】我们可借鉴以前研究函数的经验,探索函数y=x+
【探索研究】我们可借鉴以前研究函数的经验,探索函数y=x+| 1 |
| x |
| x | … |
|
|
| 1 | 2 | 3 | 4 | … | ||||||||||||
| y | … |
|
|
| 2 |
|
|
| … |
| 1 |
| x |
| x |
|
| x |
|
| x |
|
| x |
|
| x |
|
| 1 |
| x |
| 1 |
| x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com