
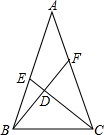
 如图,在△ABC中,AB=AC,点E、F分别在AB和AC上,CE与BF相交于点D.若AE=CF,D为BF的中点,则$\frac{AE}{AB}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,在△ABC中,AB=AC,点E、F分别在AB和AC上,CE与BF相交于点D.若AE=CF,D为BF的中点,则$\frac{AE}{AB}$的值为$\frac{\sqrt{5}-1}{2}$. 分析 过F作FH∥AB交CE于H,首先证明△BED≌△FHD(SAS),得FH=BE;再证明△CFH∽△CAE,得到HF:AE=CF:AC,由已知可得CF=AE,AF=BE=HF,设AC=BA=1,AE=x,代入相似比中,即可解得x,即可得解AE:AB.
解答 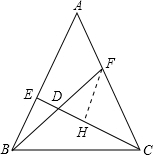 解:过F作FH∥AB交CE于H,
解:过F作FH∥AB交CE于H,
∵FH∥AB,
∴∠HFD=∠EBD,
∵D为BF的中点,
∴BD=DF,
在△BED和△FHD中,
$\left\{\begin{array}{l}{∠BED=∠FHD}\\{∠EDB=∠HDF}\\{BD=DF}\end{array}\right.$
∴△BED≌△FHD(AAS),
∴FH=BE,
∵FH∥AB,
∴△CFH∽△CAE,
∴HF:AE=CF:AC,
∵AC=AB,CF=AE,
∴AF=BE=HF,
设AC=AB=1,AE=x,则$\frac{HF}{AE}=\frac{CF}{AC}$,即为$\frac{1-x}{x}=\frac{x}{1}$,
解得x=$\frac{\sqrt{5}}{2}-\frac{1}{2}$,
∴AE:AB=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题主要考查三角形全等的判定和性质、三角形相似的判定和性质及二元一次方程的解法,正确作出辅助线是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2x2-6x+3=0 | B. | x2-4x+3=0 | C. | x2+3x-5=0 | D. | 2x2+6x+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知在Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为$\frac{1}{{2}^{2012}}$.
如图,已知在Rt△ABC中,AB=AC=3$\sqrt{2}$,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第2014个内接正方形的边长为$\frac{1}{{2}^{2012}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.
甲、乙两地相距20千米.小明上午8:30骑自行车由甲地去乙地,平均车速8千米/小时;小丽上午10:00坐公共汽车沿相同的路线也由甲地去乙地,平均车速为40千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 节能设备 | 甲型 | 乙型 |
| 价格(万元/台) | 12 | b |
| 产量(吨/月 ) | 240 | 180 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com