
【题目】如图,![]() 、
、![]() 是正方形,
是正方形,![]() 在
在![]() 上,直线
上,直线![]() 、
、![]() 交于
交于![]() ,且
,且![]() ,
,![]() 、
、![]() 交于
交于![]() ,当
,当![]() 在线段
在线段![]() (不与
(不与![]() 、
、![]() 重合)上运动时,下列四个结论:①
重合)上运动时,下列四个结论:①![]() ;②
;②![]() 、
、![]() 所夹的锐角为
所夹的锐角为![]() ;③
;③![]() ;④若
;④若![]() 平分
平分![]() ,则正方形
,则正方形![]() 的面积为4,其中结论正确的是__(填序号)
的面积为4,其中结论正确的是__(填序号)
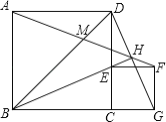
【答案】①②③④
【解析】
由已知条件可证得△BEC≌△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90°,所以∠BDC+∠DBH+∠CDG=90°,即∠BHD=90°,故①正确;由题意得![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五点都在以
五点都在以![]() 为直径的圆上,根据圆周角定理即可得到∠AHD=45°,故②正确;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的性质即可得到③正确;过
为直径的圆上,根据圆周角定理即可得到∠AHD=45°,故②正确;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的性质即可得到③正确;过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,若BE平分∠DBC,那么H是DG的中点,易证得
,若BE平分∠DBC,那么H是DG的中点,易证得![]() ,求出
,求出![]() ,然后证明
,然后证明![]() ,可得
,可得![]() ,即
,即![]() ,由此可知④正确.
,由此可知④正确.
解:① ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴∠BHD=90°,即![]() ,故①正确;
,故①正确;
②由于![]() 、
、![]() 、
、![]() 都是直角,因此
都是直角,因此![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五点都在以
五点都在以![]() 为直径的圆上,由圆周角定理知:
为直径的圆上,由圆周角定理知:![]() ,故②正确;
,故②正确;
③由②知:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五点共圆,则
五点共圆,则![]() ,
,
又![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,故③正确;
,故③正确;
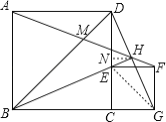
④过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ;
;
若BE平分∠DBC,且![]() ,
,
∴![]() 是
是![]() 中点,
中点,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() 为
为![]() 的中位线,
的中位线,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,即
,即![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,即正方形
,即正方形![]() 的面积为4,故④正确;
的面积为4,故④正确;
故答案为:①②③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有
“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.

(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农场老板准备建造一个矩形羊圈![]() ,他打算让矩形羊圈的一面完全靠着墙
,他打算让矩形羊圈的一面完全靠着墙![]() ,墙
,墙![]() 可利用的长度为
可利用的长度为![]() ,另外三面用长度为
,另外三面用长度为![]() 的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)

![]() 若要使矩形羊圈的面积为
若要使矩形羊圈的面积为![]() ,则垂直于墙的一边长
,则垂直于墙的一边长![]() 为多少米?
为多少米?
![]() 农场老板又想将羊圈
农场老板又想将羊圈![]() 的面积重新建造成面积为
的面积重新建造成面积为![]() ,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
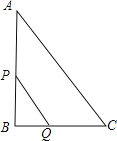
【题目】如图,Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以2cm/s的速度,沿AB向终点B移动;点Q以1cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连接PQ.设动点运动时间为x秒.
(1)用含x的代数式表示BQ、PB的长度;
(2)当x为何值时,△PBQ为等腰三角形;
(3)是否存在x的值,使得四边形APQC的面积等于20cm2?若存在,请求出此时x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
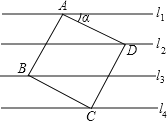
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
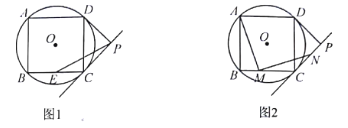
【题目】如图,四边形![]() 是
是![]() 的内接正方形,
的内接正方形,![]() ,
,![]() 、
、![]() 是
是![]() 的两 条切线,
的两 条切线,![]() 、
、![]() 为切点.
为切点.
(1)如图1,求![]() 的半径;
的半径;
(2)如图1,若点![]() 是
是![]() 的中点,连结
的中点,连结![]() ,求
,求![]() 的长度;
的长度;
(3)如图2,若点![]() 是
是![]() 边上任意一点(不含
边上任意一点(不含![]() 、
、![]() ),以点
),以点![]() 为直角顶点,在
为直角顶点,在![]() 的上方作
的上方作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
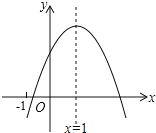
A.abc<0B.2a+b=0C.b2﹣4ac>0D.a﹣b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() 为定长,以
为定长,以![]() 为直径的
为直径的![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .联结
.联结![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 点到
点到![]() 的距离不变;③
的距离不变;③![]() ;④
;④![]() 为外接圆的切线.其中正确的结论是( )
为外接圆的切线.其中正确的结论是( )
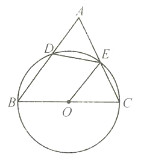
A.①②B.③④C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张相同的卡片,分别写有数字![]() 2,0,1,5,将它们背面朝上(背面无差别)洗匀后放在桌上.
2,0,1,5,将它们背面朝上(背面无差别)洗匀后放在桌上.
(1)从中任意抽出一张,抽到卡片上的数字为负数的概率;
(2)从中任意抽出两张,用树状图或表格列出所有可能的结果,并求抽出卡片上的数字积为正数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com