
【题目】已知P(a,y1),Q(1,y2)是抛物线y=kx2+(2k+1)x+2(k是不等于0的常数)上的两点.
(1)求证:无论k取任何实数时,关于x的方程kx2+(2k+1)x+2=0总有实数根;
(2)当k=1时,
①求抛物线y=kx2+(2k+1)x+2图象与x轴两个交点坐标,并画出此条抛物线的草图;
②若y1>y2,请结合函数图象确定实数a的取值范围.
【答案】(1)见解析;(2)①(﹣2,0)、(﹣1,0),作图见解析;②a<﹣4或a>1
【解析】
(1)计算![]() 的值,根据
的值,根据![]() ≥0可得结论;
≥0可得结论;
(2)①先将k=1代入得:y=x2+3x+2,令y=0可以计算抛物线与x轴两个交点坐标,并画出抛物线;
②根据图象找到Q关于对称轴的对称点A的坐标,可得a的取值范围.
解:(1)kx2+(2k+1)x+2=0,
![]() =(2k+1)2﹣4k×2=4k2+4k+1﹣8k=4k2﹣4k+1=(2k﹣1)2≥0,
=(2k+1)2﹣4k×2=4k2+4k+1﹣8k=4k2﹣4k+1=(2k﹣1)2≥0,
∴无论k取任何实数时,关于x的方程kx2+(2k+1)x+2=0总有实数根;
(2)①当k=1时,y=kx2+(2k+1)x+2=x2+3x+2,
当y=0时,x2+3x+2=0,
(x+1)(x+2)=0,
x1=﹣1,x2=﹣2,
∴抛物线y=kx2+(2k+1)x+2图象与x轴两个交点坐标分别为(﹣2,0)、(﹣1,0),
列表如下:
x | -4 | -3 | -2 | - | -1 | 0 | 1 |
y | 6 | 2 | 0 | ﹣ | 0 | 2 | 6 |
描点、连线可得抛物线的草图如图所示:
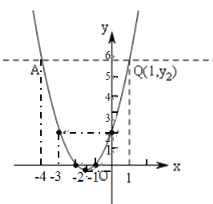
②由y=x2+3x+2=(x+![]() )2﹣
)2﹣![]() 可知,
可知,
∴抛物线的对称轴是:x=﹣![]() .
.
由对称性得:点Q关于抛物线的对称轴对称的点A的坐标为(﹣4,y2),
∵P(a,y1),Q(1,y2)
∴若y1>y2,实数a的取值范围是a<﹣4或a>1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
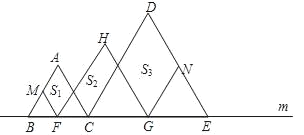
【题目】如图,在直线m上摆放着三个正三角形:△ABC,△HFG,△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=___________.
CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
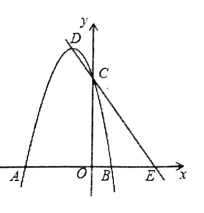
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]()
(1)求抛物线的顶点坐标(用含![]() 的式子表示);
的式子表示);
(2)![]() 的长是否与
的长是否与![]() 值有关,说明你的理由;
值有关,说明你的理由;
(3)设![]() ,求
,求![]() 的取值范围;
的取值范围;
(4)以![]() 为斜边,在直线
为斜边,在直线![]() 的左下方作等腰直角三角形
的左下方作等腰直角三角形![]() .设
.设![]() ,直接写出
,直接写出![]() 关于
关于![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
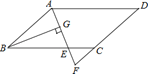
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=![]() ,则△CEF的面积是( )
,则△CEF的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
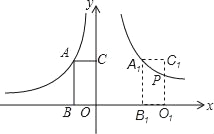
【题目】如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣![]() (x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=
(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=![]() (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
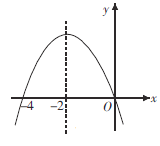
【题目】如图是二次函数![]() 图像的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②
图像的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②![]() ;③
;③![]() ;④
;④![]() ;⑤方程
;⑤方程![]() 的两个根为
的两个根为![]() ,
,![]() 其中正确的结论有( )
其中正确的结论有( )
A.①③④B.②④⑤C.①②⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
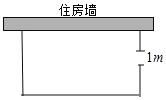
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛. 并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级:A:优秀,B:良好,C:一般,D:较差),并制作了如下统计图表(部分信息未给出):
等级 | 人数 |
A | m |
B | 20 |
C | n |
D | 10 |

请根据统计图表中的信息解答下列问题:
(1)这次共抽取了________名参加演讲比赛的学生,统计图中a=________,b=________;
(2)若该校学生共有2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的有多少人?
(3)若演讲比赛成绩为A等级的学生中恰好有2名女生,其余的学生为男生,从A等级的学生中抽取两名同学参加全市演讲比赛,求抽中一名男生和一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com