
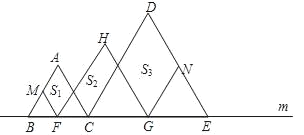
【题目】如图,在直线m上摆放着三个正三角形:△ABC,△HFG,△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=___________.
CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=___________.
【答案】4
【解析】
根据题意,可以证明S1与S2两个平行四边形的高相等,S2长是S1的2倍,S3与S2的长相等,高S3的一半,这样就可以把S1和S3用S2来表示,从而计算出S2的值.
解:根据正三角形的性质,∠ABC=∠HFG=∠DCE=60°,
∴AB∥HF∥DC∥GN,
设AC与FH交于P,CD与HG交于Q,
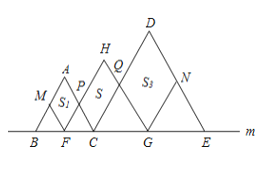
∴△PFC、△QCG和△NGE是正三角形,
∵F、G分别是BC、CE的中点,
∴MF=![]() AC=
AC=![]() BC,PF=
BC,PF=![]() AB=
AB=![]() BC,
BC,
又∵BC=![]() CE=CG=GE,
CE=CG=GE,
∴CP=MF,CQ=BC,QG=GC=CQ=AB,
∴S1=![]() S2,S3=2S2,
S2,S3=2S2,
∵S1+ S3=10,
∴![]() S2+2S2=10,
S2+2S2=10,
∴S2=4;
故答案为:S2=4;


科目:初中数学 来源: 题型:
【题目】一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为____________海里/时.
查看答案和解析>>
科目:初中数学 来源: 题型:
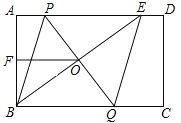
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
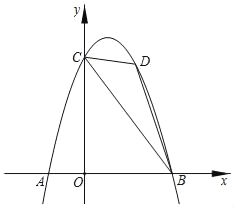
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC,DB,DC.
(1)求抛物线的函数解析式;
(2)△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点P是CD上一动点,连结PA,分别过点B、D作BE⊥PA、DF⊥PA,垂足为E、F,如图①.
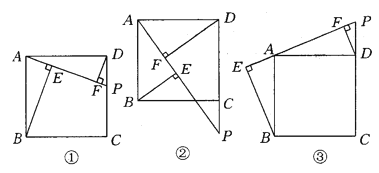
(1)请探索BE、DF、EF这三条线段长度具有怎样的数量关系,若点P在DC的延长线上(如图②),那么这三条线段的长度之间又有怎样的数量关系?若点P在CD的延长线上呢(如图③)?请分别直接写出结论.
(2)请在(1)中的三个结论中选择一个加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
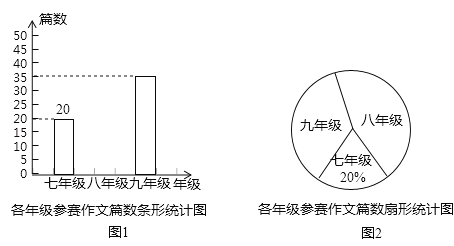
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我省部分地区遭遇严重干旱,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.
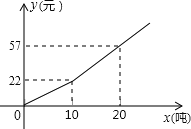
(1)小聪家五月份用水7吨,应交水费 元;
(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(a,y1),Q(1,y2)是抛物线y=kx2+(2k+1)x+2(k是不等于0的常数)上的两点.
(1)求证:无论k取任何实数时,关于x的方程kx2+(2k+1)x+2=0总有实数根;
(2)当k=1时,
①求抛物线y=kx2+(2k+1)x+2图象与x轴两个交点坐标,并画出此条抛物线的草图;
②若y1>y2,请结合函数图象确定实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com